【题目】如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.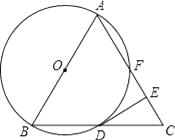
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.
参考答案:
【答案】
(1)证明:如图1,连接OD,
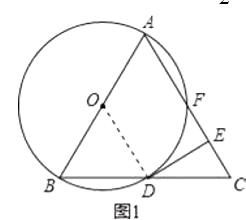
∵△ABC是等边三角形,
∴∠B=∠C=60°.
∵OB=OD,
∴∠ODB=∠B=60°.
∵DE⊥AC,
∴∠DEC=90°.
∴∠EDC=30°.
∴∠ODE=90°.
∴DE⊥OD于点D.
∵点D在⊙O上,
∴DE是⊙O的切线
(2)解:如图2,连接AD,BF,
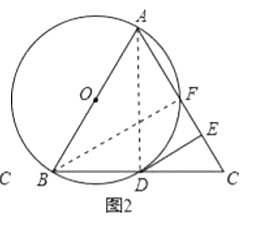
∵AB为⊙O直径,
∴∠AFB=∠ADB=90°.
∴AF⊥BF,AD⊥BD.
∵△ABC是等边三角形,
∴ ![]() ,
, ![]() .
.
∵∠EDC=30°,
∴ ![]() .∴FE=FC﹣EC=1
.∴FE=FC﹣EC=1
【解析】(1)要证切线,可连半径,证垂直,由已知得出O、D是中点,利用中位线定理即得DE⊥OD于点D;(2)利用直径的性质,须连BF ,求出FC,EC,进而FE=FC﹣EC=1.
【考点精析】关于本题考查的圆周角定理,需要了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC,AB=AC=5,BC=6,若点P在边AC上移动,则BP的最小值是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,正比例函数
中,正比例函数  与反比例函数
与反比例函数  的图象交于A,B两点,点A的横坐标为2,AC⊥x轴于点C,连接BC.
的图象交于A,B两点,点A的横坐标为2,AC⊥x轴于点C,连接BC.
(1)求反比例函数的表达式;
(2)若点P是反比例函数 图象上的一点,且满足△OPC的面积是△ABC面积的一半,请直接写出点P的坐标.
图象上的一点,且满足△OPC的面积是△ABC面积的一半,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次户外研学活动中,老师带领学生去测一条东西流向的河流的宽度(把河两岸看做平行线,河宽即两岸之间的垂线段的长度).某同学在河南岸A处观测到河对岸水边有一棵树P,测得P在A北偏东60°方向上,沿河岸向东前行20米到达B处,测得P在B北偏东45°方向上.求河宽(结果保留一位小数.
 ,
,  ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据几何图形的面积关系可以形象直观地表示多项式的乘法.例如:(2a+b)(a+b)=2a2+3ab+b2可以用图(1)表示
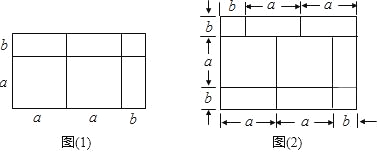
(1)根据图(2),写出一个多项式乘以多项式的等式;
(2)从A,B两题中任选一题作答:
A.请画出一个几何图形,表示(x+p)(x+q)=x2+(p+q)x+pq,并仿照上图标明相应的字母;
B.请画出一个几何图形,表示(x﹣p)(x﹣q)=x2﹣(p+q)x+pq,并仿照上图标明相应的字母.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑自行车上学,某天他从家出发骑行了一段路程,想起要买一本书,于是折回到他刚经过的某书店,买到书后继续去学校.以下是他在本次上学离家的距离与所用的时间的关系示意图,根据图中提供的信息解答下列问题:
(1)小明家与学校的距离是_____米.
(2)小明在书店停留了多少分钟?
(3)从A,B两题中任选一题作答:
A.小明骑行过程中哪个时间段的速度最快,最快的速度是多少?
B.小明在这次上学过程中的平均速度是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,按以下步骤作图:
①以B为圆心,任意长为半径作弧,交AB于D,交BC于E;
②分别以D,E为圆心,以大于
 DE的同样长为半径作弧,两弧交于点F;
DE的同样长为半径作弧,两弧交于点F; ③作射线BF交AC于G.
如果BG=CG,∠A=60°,那么∠ACB的度数为____________.

相关试题

