【题目】在△ABC,AB=AC=5,BC=6,若点P在边AC上移动,则BP的最小值是_______.
参考答案:
【答案】4.8
【解析】
根据点到直线的连线中,垂线段最短,得到当BP垂直于AC时,BP的长最小,过A作等腰三角形底边上的高AD,利用三线合一得到D为BC的中点,在直角三角形ADC中,利用勾股定理求出AD的长,进而利用面积法即可求出此时BP的长.
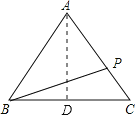
解:根据垂线段最短,得到BP⊥AC时,BP最短,
过A作AD⊥BC,交BC于点D,
∵AB=AC,AD⊥BC,
∴D为BC的中点,又BC=6,
∴BD=CD=3,
在Rt△ADC中,AC=5,CD=3,
根据勾股定理得:AD=![]() =4,
=4,
又∵S△ABC=![]() BCAD=
BCAD=![]() BPAC,
BPAC,
∴BP=![]() =
=![]() =4.8.
=4.8.
故答案为:4.8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.

(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=
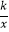 的图象上,过点A的直线y=x+b交x轴于点B.
的图象上,过点A的直线y=x+b交x轴于点B.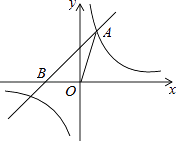
(1)求k和b的值;
(2)求△OAB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠A,∠B,∠C的对边分别为a、b、c,下列说法中错误的是( )
A.如果∠C-∠B=∠A,则△ABC是直角三角形,且∠C=90;
B.如果
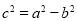 ,则△ABC是直角三角形,且∠C=90;
,则△ABC是直角三角形,且∠C=90;C.如果(c+a)( c-a)=
 ,则△ABC是直角三角形,且∠C=90;
,则△ABC是直角三角形,且∠C=90;D.如果∠A:∠B:∠C=3:2:5,则△ABC是直角三角形,且∠C=90.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列解题过程,然后回答问题:
解方程:

解:①当
 ≥0时,原方程可化为:
≥0时,原方程可化为:  ,解得
,解得 ;
;②当
 <0时,原方程可化为:
<0时,原方程可化为:  ,解得
,解得 ;
;所以原方程的解是
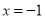 或
或
(1)解方程:

(2)探究:当
 为何值时,方程
为何值时,方程 ①无解;②只有一个解;③有两个解。
①无解;②只有一个解;③有两个解。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A,点B,点C表示的数分别为﹣2,1,6.

(1)线段AB的长度为 个单位长度,线段AC的长度为 个单位长度.
(2)点P是数轴上的一个动点,从A点出发,以每秒1个单位长度的速度,沿数轴的正方向运动,运动时间为t秒(0≤t≤8).用含t的代数式表示:线段BP的长为 个单位长度,点P在数轴上表示的数为 ;
(3)点M,点N都是数轴上的动点,点M从点A出发以每秒4个单位长度的速度运动,点N从点C出发以每秒3个单位长度的速度运动.设点M,N同时出发,运动时间为x秒.点M,N相向运动,当点M,N两点间的距离为13个单位长度时,求x的值,并直接写出此时点M在数轴上表示的数.
相关试题

