【题目】小明骑自行车上学,某天他从家出发骑行了一段路程,想起要买一本书,于是折回到他刚经过的某书店,买到书后继续去学校.以下是他在本次上学离家的距离与所用的时间的关系示意图,根据图中提供的信息解答下列问题:
(1)小明家与学校的距离是_____米.
(2)小明在书店停留了多少分钟?
(3)从A,B两题中任选一题作答:
A.小明骑行过程中哪个时间段的速度最快,最快的速度是多少?
B.小明在这次上学过程中的平均速度是多少?

参考答案:
【答案】(1)1500;(2)小明在书店停留了4分钟;(3)A:小明骑行过程中在12﹣14分钟这个时间段内速度最快,最快速度是450米/分钟;B:小明在这次上学过程中的平均速度是![]() 米/分钟.
米/分钟.
【解析】
(1)根据函数图象可以解答本题;
(2)根据函数图象中的数据可以解答本题;
(3)根据题意可以分别对选择A和B进行作答.
(1)由图可得:小明家与学校的距离是1500米.
故答案为:1500;
(2)由图可得:小明在书店停留了12﹣8=4(分钟),即小明在书店停留了4分钟;
(3)选A:设小明骑行的时间为t,路程为S,当0<t≤6时,速度为:1200÷6=200(米/分钟),当6<t≤8时,速度为:(1200﹣600)÷(8﹣6)=300(米/分钟),当12≤t≤14时,速度为:(1500﹣600)÷(14﹣12)=450(米/分钟),∴小明骑行过程中在12﹣14分钟这个时间段内速度最快,最快速度是450米/分钟;
选B:小明在这次上学过程中的平均速度是:(1200+600+900)÷14![]() (米/分钟),即小明在这次上学过程中的平均速度是
(米/分钟),即小明在这次上学过程中的平均速度是![]() 米/分钟.
米/分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次户外研学活动中,老师带领学生去测一条东西流向的河流的宽度(把河两岸看做平行线,河宽即两岸之间的垂线段的长度).某同学在河南岸A处观测到河对岸水边有一棵树P,测得P在A北偏东60°方向上,沿河岸向东前行20米到达B处,测得P在B北偏东45°方向上.求河宽(结果保留一位小数.
 ,
,  ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
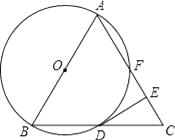
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据几何图形的面积关系可以形象直观地表示多项式的乘法.例如:(2a+b)(a+b)=2a2+3ab+b2可以用图(1)表示
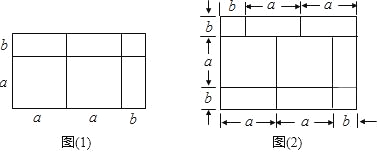
(1)根据图(2),写出一个多项式乘以多项式的等式;
(2)从A,B两题中任选一题作答:
A.请画出一个几何图形,表示(x+p)(x+q)=x2+(p+q)x+pq,并仿照上图标明相应的字母;
B.请画出一个几何图形,表示(x﹣p)(x﹣q)=x2﹣(p+q)x+pq,并仿照上图标明相应的字母.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,按以下步骤作图:
①以B为圆心,任意长为半径作弧,交AB于D,交BC于E;
②分别以D,E为圆心,以大于
 DE的同样长为半径作弧,两弧交于点F;
DE的同样长为半径作弧,两弧交于点F; ③作射线BF交AC于G.
如果BG=CG,∠A=60°,那么∠ACB的度数为____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:过点A的射线l⊥AB,在射线l上截取线段AC=AB,过 A的直线m不与直线l及直线AB重合,过点B作BD⊥m于点D,过点C作CE⊥m于点E.
(1)依题意补全图形;
(2)求证:△AEC≌△BDA.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在Rt△ABC中,∠C=90°.将△ABC绕点C逆时针旋转得到△A’B’C,旋转角为
 ,且0°<
,且0°<  <180°.在旋转过程中,点B’可以恰好落在AB的中点处,如图②.
<180°.在旋转过程中,点B’可以恰好落在AB的中点处,如图②.
(1)求∠A的度数;
(2)当点C到AA’的距离等于AC的一半时,求 的度数.
的度数.
相关试题

