搜索
【题目】如图，在△ABC中，按以下步骤作图：
①以B为圆心，任意长为半径作弧，交AB于D，交BC于E；
②分别以D，E为圆心，以大于
DE的同样长为半径作弧，两弧交于点F；
③作射线BF交AC于G.
如果BG=CG，∠A=60°，那么∠ACB的度数为____________．
参考答案：
【答案】40°
【解析】
由作图可知，BG平分∠ABC，得到∠ABG=∠CBG，由等边对等角得到∠CBG=∠BCG，再由三角形内角和定理即可得到结论．
由作图可知，BG平分∠ABC，∴∠ABG=∠CBG．
∵BG=CG，∴∠CBG=∠BCG．
∵∠A+∠ACB +∠CBA=180°，∴∠A+3∠ACB =180°，∴60°+3∠ACB =180°，∴∠ACB =40°．
故答案为：40°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC是等边三角形，以AB为直径作⊙O，交BC边于点D，交AC边于点F，作DE⊥AC于点E．
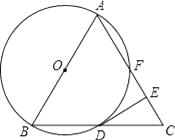
（1）求证：DE是⊙O的切线；
（2）若△ABC的边长为4，求EF的长度． -
科目： 来源： 题型：
查看答案和解析>>【题目】根据几何图形的面积关系可以形象直观地表示多项式的乘法．例如：(2a+b)(a+b)＝2a2+3ab+b2可以用图(1)表示
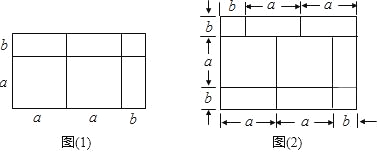
(1)根据图(2)，写出一个多项式乘以多项式的等式；
(2)从A，B两题中任选一题作答：
A．请画出一个几何图形，表示(x+p)(x+q)＝x2+(p+q)x+pq，并仿照上图标明相应的字母；
B．请画出一个几何图形，表示(x﹣p)(x﹣q)＝x2﹣(p+q)x+pq，并仿照上图标明相应的字母．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明骑自行车上学，某天他从家出发骑行了一段路程，想起要买一本书，于是折回到他刚经过的某书店，买到书后继续去学校．以下是他在本次上学离家的距离与所用的时间的关系示意图，根据图中提供的信息解答下列问题：
(1)小明家与学校的距离是_____米．
(2)小明在书店停留了多少分钟？
(3)从A，B两题中任选一题作答：
A．小明骑行过程中哪个时间段的速度最快，最快的速度是多少？
B．小明在这次上学过程中的平均速度是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：过点A的射线l⊥AB，在射线l上截取线段AC=AB，过 A的直线m不与直线l及直线AB重合，过点B作BD⊥m于点D,过点C作CE⊥m于点E.
（1）依题意补全图形；
（2）求证：△AEC≌△BDA.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，在Rt△ABC中，∠C=90°．将△ABC绕点C逆时针旋转得到△A’B’C，旋转角为
，且0°< <180°．在旋转过程中，点B’可以恰好落在AB的中点处，如图②．
（1）求∠A的度数；
（2）当点C到AA’的距离等于AC的一半时，求
的度数． -
科目： 来源： 题型：
查看答案和解析>>【题目】有这样一个问题：探究函数
的图象与性质．
小慧根据学习函数的经验，对函数的图象与性质进行了探究．
下面是小慧的探究过程，请补充完成：
（1）函数的自变量x的取值范围是；
（2）列出y与x的几组对应值．请直接写出m的值，m=；x
…
-3
-2
0
1
1．5
2．5
m
4
6
7
…
y
…
2．4
2．5
3
4
6
-2
0
1
1．5
1．6
…
（3）请在平面直角坐标系
， 描出以上表中各对对应值为坐标的点，并画出该函数的图象；
（4）结合函数的图象，写出该函数的两条性质：
①；
② ．
相关试题
