搜索
【题目】如图，在△ABC中，AD⊥BC，AB=10，BD=8，∠ACD=45°．
（1）求线段AD的长；
（2）求△ABC的周长．
参考答案：
【答案】（1）6；（2）
.
【解析】
（1）由AD⊥BC可得出∠ADB=90°，在Rt△ABD中，利用勾股定理即可求出AD的长；
（2）由AD⊥BC、∠ACD=45°可得出△ACD为等腰直角三角形，结合AD的长度可得出CD、AC的长度，再利用周长的定理即可求出△ABC的周长．
解：（1）∵AD⊥BC，
∴∠ADB=90°．
在Rt△ABD中，∠ADB=90°，AB=10，BD=8，
∴AD=
=6．
（2）∵AD⊥BC，∠ACD=45°，
∴△ACD为等腰直角三角形，
又∵AD=6，
∴CD=6，AC=6
，
∴C△ABC=AB+BD+CD+AC=24+6．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，AE是高，AF是△ABC外角∠CAD的平分线．
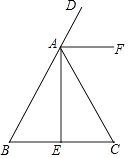
（1）用尺规作图：作∠AEC的平分线EN（保留作图痕迹，不写作法和证明）；
（2）设EN与AF交于点M，判断△AEM的形状，并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙、丙三人之间相互传球，球从一个人手中随机传到另外一个人手中，共传球三次．
（1）若开始时球在甲手中，求经过三次传球后，球传回到甲手中的概率是多少？
（2）若丙想使球经过三次传递后，球落在自己手中的概率最大，丙会让球开始时在谁手中？请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：关于x的一元二次方程tx2﹣（3t+2）x+2t+2=0（t＞0）
（1）求证：方程有两个不相等的实数根；
（2）设方程的两个实数根分别为x1 ， x2（其中x1＜x2），若y是关于t的函数，且y=x2﹣2x1 ， 求这个函数的解析式，并画出函数图象；
（3）观察（2）中的函数图象，当y≥2t时，写出自变量t的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以Rt△ABC的AC边为直径作⊙O交斜边AB于点E，连接EO并延长交BC的延长线于点D，点P为BC的中点，连接EP，AD．
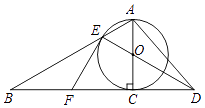
（1）求证：PE是⊙O的切线；
（2）若⊙O的半径为3，∠B=30°，求P点到直线AD的距离． -
科目： 来源： 题型：
查看答案和解析>>【题目】下表是小华同学一个学期数学成绩的记录．根据表格提供的信息，回答下列的问题：
考试类别
平时考试
期中考试
期末考试
第一单元
第二单元
第三单元
第四单元
成绩（分）
85
78
90
91
90
94
（1）小明6次成绩的众数是 ，中位数是 ；
（2）求该同学这个同学这一学期平时成绩的平均数；
（3）总评成绩权重规定如下：平时成绩占20%，期中成绩占30%，期末成绩占50%，请计算出小华同学这一个学期的总评成绩是多少分？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知：在Rt△ABC中，斜边AB=10，sinA=
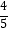，点P为边AB上一动点（不与A，B重合），PQ平分∠CPB交边BC于点Q，QM⊥AB于M，QN⊥CP于N．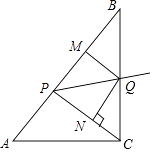
（1）当AP=CP时，求QP；
（2）若四边形PMQN为菱形，求CQ；
（3）探究：AP为何值时，四边形PMQN与△BPQ的面积相等？
相关试题
