【题目】甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.
(1)若开始时球在甲手中,求经过三次传球后,球传回到甲手中的概率是多少?
(2)若丙想使球经过三次传递后,球落在自己手中的概率最大,丙会让球开始时在谁手中?请说明理由.
参考答案:
【答案】
(1)解:画树状图如图所示,
三次传球有8种等可能结果,其中传回甲手中的有2种,即甲→乙→丙→甲,甲→丙→乙→甲,
∴经过三次传球后,球传回到甲手中的概率为 ![]() =
= ![]() .
.

(2)解:由树状图可知:从甲开始传球,传球三次后传到丙手中的概率为 ![]() ,
,
同理:从乙开始传球,传球三次后传到丙手中的概率为 ![]() ,从丙自己开始传球,传球三次后传到丙手中的概率为
,从丙自己开始传球,传球三次后传到丙手中的概率为 ![]() =
= ![]() ,
,
∴丙想使球经过三次传递后,球落在自己手中的概率最大,丙会让球开始时在甲或乙手中.
【解析】(1)依照题意画出树状图,根据树状图即可得出经过三次传球后球传回到甲手中的概率;(2)结合(1)的树状图,可得出从甲开始传球传球三次后传到丙手中的概率,同理,可得出从乙、丙开始传球,三次传球后传到丙手中的概率,对比后即可得出结论.
【考点精析】关于本题考查的列表法与树状图法,需要了解当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点P,Q分别为AD,CD边上的点,且DQ=CP,连接BQ,AP.求证:BQ=AP.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题.

(1)将下面的表格补充完整:
正多边形的边数
3
4
5
6
……
18
∠α的度数
……
(2)根据规律,是否存在一个正n边形,使其中的∠α=20°?若存在,直接写出n的值;若不存在,请说明理由.
(3)根据规律,是否存在一个正n边形,使其中的∠α=21°?若存在,直接写出n的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AE是高,AF是△ABC外角∠CAD的平分线.
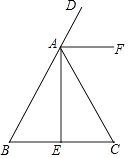
(1)用尺规作图:作∠AEC的平分线EN(保留作图痕迹,不写作法和证明);
(2)设EN与AF交于点M,判断△AEM的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的一元二次方程tx2﹣(3t+2)x+2t+2=0(t>0)
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为x1 , x2(其中x1<x2),若y是关于t的函数,且y=x2﹣2x1 , 求这个函数的解析式,并画出函数图象;
(3)观察(2)中的函数图象,当y≥2t时,写出自变量t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,AB=10,BD=8,∠ACD=45°.
(1)求线段AD的长;
(2)求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点P为BC的中点,连接EP,AD.
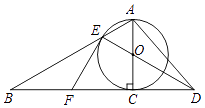
(1)求证:PE是⊙O的切线;
(2)若⊙O的半径为3,∠B=30°,求P点到直线AD的距离.
相关试题

