【题目】如图1,矩形ABCD,E为边AB上的点,将△BCE沿CE折叠,点B恰好落在AC上点B′处.

(1)若AB=8,BC=6,求BE的长度;
(2)如图2,过点D作EC的垂线,垂足为点G,分别交BC、AC于点F、H,连结EF,若EF=AE,求证:![]() 为定值;
为定值;
(3)若四边形EFCH是菱形,则![]() =_____.
=_____.
参考答案:
【答案】(1)3;(2)证明见解析,![]() ;(3)
;(3)![]()
【解析】
(1)由轴对称的性质可知BE=BE',∠AB'E=90°,可设BE=BE'=x,通过勾股定理可求出BE的长;
(2)先证∠AEB'=∠ACB,再证∠EFB=∠AEB'=∠ACB并设为![]() ,设∠EFD=
,设∠EFD=![]() ,可通过平角等于180°列出等量关系式,求出β与α的比值,即可求出结果;
,可通过平角等于180°列出等量关系式,求出β与α的比值,即可求出结果;
(3)设EF=FC=CH=HE=a,AD=y,证△ADH∽△CFH,求出AD=AH=b,通过△AEH∽△ABC可求出a与b的关系,即可求出最终结论.
解:(1)如图:

∵四边形ABCD为矩形,
∴△ABC为直角三角形,
Rt△ABC中,由勾股定理,
![]() ,
,
由翻折可知:BC=B′C=6,
∴AB′=10-6=4,
设EB=EB′=x,AE=8-x,
Rt△AEB′中,AB′2+EB′2=AE2,
∴42+x2=(8-x)2,
∴x=3,
∴BE=3;
(2)作![]() ,如图:
,如图:

在△AB'E与△ABC中,∠AB'E=∠B=90°,∠EAB'=∠CAB,
∴∠AEB'=∠ACB,
∵BE=B'E,EF=AE,∠AB'E=∠B,
∴Rt△AB'E≌Rt△FBE(HL),
∴∠EFB=∠AEB',
设∠EFB=∠AEB'=∠ACB=![]() ,∠EFD=
,∠EFD=![]() ,
,
则∠FEG=90°-![]() ,
,
∴∠BEC=![]() +90°-
+90°-![]() ,
,
由折叠知,∠BEC=∠B'EC,
∵∠BEC+∠B'EC+∠AEB'=90°,
∴2(![]() +90°
+90°![]() )+
)+![]() =180°,
=180°,
∴3![]() =2
=2![]() ,
,
∴![]() ,
,
即![]() 为定值
为定值![]() ;
;
(3)如图:

设EF=FC=CH=HE=a,AD=y,
∵AD∥BC,
∴△ADH∽△CFH,
∴![]() ,
,
∵CF=CH,
∴AD=AH=b,
∴AC=a+b,
∵EH∥BC,
∴△AEH∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
设b=1,则![]() ,
,
∴ ,
,
∴![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的对角线交于点E,将△DCB沿CD翻折得到△DCF.
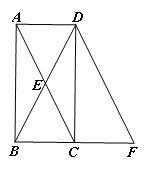
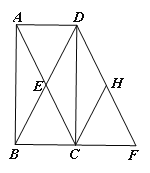
(1)求证:四边形ACFD是平行四边形;
(2)点H为DF的中点,连结CH,若AB=4,BC=2,求四边形ECHD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在10×10网格中,点A和直线l的位置如图所示:

(1)将点A向右平移6个单位,再向上平移2个单位长度得到点B,在网格中标出点B;
(2)在(1)的条件下,在直线l上确定一点P,使PA+PB的值最小,保留画图痕迹,并直接写出PA+PB的最小值:______;
(3)结合(2)的画图过程并思考,直接写出
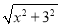 +
+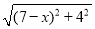 的最小值:____
的最小值:____ -
科目: 来源: 题型:
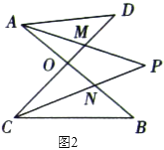
查看答案和解析>>【题目】如图
 ,线段
,线段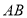 、
、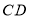 相交于
相交于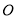 ,连结
,连结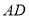 、
、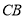 ,我们把形如图
,我们把形如图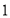 的图形称之为“
的图形称之为“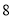 ”字形,如图
”字形,如图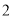 ,在图
,在图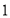 的条件下,
的条件下,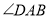 和
和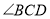 的平分线
的平分线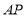 和
和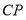 相交于点
相交于点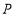 ,并且与
,并且与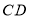 、
、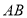 分别相交于
分别相交于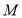 、
、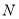 ,试解答下列问题:
,试解答下列问题: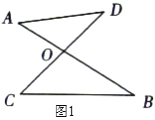
(1)在图
 中,请直接写出
中,请直接写出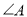 、
、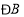 、
、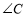 、
、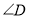 之间的数量关系:__________
之间的数量关系:__________(2)仔细观察,在图
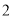 中“
中“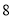 ”字形的个数:______个;
”字形的个数:______个;(3)图
 中,当
中,当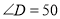 度,
度,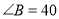 度时,求
度时,求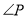 的度数.
的度数.(4)图
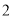 中
中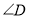 和
和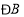 为任意角时,其它条件不变,试问
为任意角时,其它条件不变,试问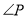 与
与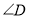 、
、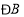 之间存在着怎样的数量关系?(直接写出结果,不必证明)
之间存在着怎样的数量关系?(直接写出结果,不必证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市民营经济持续发展,2017年城镇民营企业就业人数突破20万.为了解城镇民营企业员工每月的收入状况,统计局对全市城镇民营企业员工2017年月平均收入随机抽样调查,将抽样的数据按“2000元以内”、“2000元~4000元”、“4000元~6000元”和“6000元以上”分为四组,进行整理,分别用A,B,C,D表示,得到下列两幅不完整的统计图.
由图中所给出的信息解答下列问题:
(1)本次抽样调查的员工有 .人,在扇形统计图中x 的值为 .,表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是 .;
(2)将不完整的条形图补充完整,并估计该市2017年城镇民营企业20万员工中,每月的收入在“2000元~4000元”的约多少人?

相关试题

