【题目】对数轴上的点![]() 进行如下操作:先把点
进行如下操作:先把点![]() 表示的数乘以3,再把所得数对应的点向左平移1个单位,得到点
表示的数乘以3,再把所得数对应的点向左平移1个单位,得到点![]() 的对应点
的对应点![]() .比如,点
.比如,点![]() 表示3,3乘以3得9,表示9的点向左平移1个单位为8,因此点
表示3,3乘以3得9,表示9的点向左平移1个单位为8,因此点![]() 的对应点
的对应点![]() 表示的数为8.
表示的数为8.
⑴点![]() ,
,![]() 在数轴上,对线段
在数轴上,对线段![]() 上的每个点进行上述操作后得到线段
上的每个点进行上述操作后得到线段![]() ,其中点
,其中点![]() ,
,![]() 的对应点分别为
的对应点分别为![]() ,
,![]() .如图,若点
.如图,若点![]() 表示的数是1,则点
表示的数是1,则点![]() 表示的数是__________;若点
表示的数是__________;若点![]() 表示的数是
表示的数是![]() ,则点
,则点![]() 表示的数是__________.
表示的数是__________.
⑵若数轴上的点![]() 经过上述操作后,位置不变,则点
经过上述操作后,位置不变,则点![]() 表示的数是__________.
表示的数是__________.
![]()
参考答案:
【答案】2 1 ![]()
【解析】
(1)根据操作步骤可得出A'表示的数,设点B表示的数为x,则3x-1=-4,得出点B表示的数;
(2)设点M表示的数为y,则3y-1=y,解出即可得出M表示的数.
(1)点A′表示的数是:1×31=2;设点B表示的数为x,则3x1=4,解得:x=1,若点B′表示的数是:4,则点B表示的数是1;
(2)设点M表示的数为y,则3y1=y,解得:y=![]() ,即点M表示的数是:
,即点M表示的数是:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=kx+k﹣2经过点(m,n+1)和(m+1,2n+3),且﹣2<k<0,则n的取值范围是( )
A. ﹣2<n<0B. ﹣4<n<﹣2C. ﹣4<n<0D. 0<n<﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校要从甲乙两名射击运动员中挑选一人参加全市比赛,在选拔赛中,每人进行了5次射击,甲的成绩(环)为:9.7,10,9.6,9.8,9.9;乙的成绩的平均数为9.8,方差为0.032;
(1)甲的射击成绩的平均数和方差分别是多少?
(2)据估计,如果成绩的平均数达到9.8环就可能夺得金牌,为了夺得金牌,应选谁参加比赛?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是中国电信两种“4G套餐”计费方式.(月基本费固定收,主叫不超过主叫时间,流量不超上网流量不再收取额外费用费,主叫超时和上网超流量部分加收超时费和超流量费)

(1)若某月小萱主叫通话时间为220分钟,上网流量为800 MB,则她按套餐1计费需 元,按套餐2计费需 元;若某月小花按套餐2计费需129元,主叫通话时间为240分钟,则上网流量为 MB.
(2)若上网流量为540 MB,是否存在某主叫通话时间t(分钟),按套餐1和套餐2的计费相等?若存在,请求出t的值;若不存在,请说明理由.
(3)上网流量为540 MB,直接写出当月主叫通话时间t(分钟)满足什么条件时,选择套餐1省钱?当每月主叫通话时间t(分钟)满足什么条件时,选择套餐2省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读理解)若数轴上两点A、B所表示的数分别为a和b,则有
①A、B两点的中点表示的数为
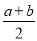 ;
;②当b>a时,A、B两点间的距离为AB=b﹣a.
(解决问题)数轴上两点A、B所表示的数分别为a和b,且满足|a+2|+(b﹣8)2020=0
(1)求出A、B两点的中点C表示的数;
(2)点D从原点O点出发向右运动,经过2秒后点D到A点的距离是点D到C点距离的2倍,求点D的运动速度是每秒多少个单位长度?
(数学思考)(3)点E以每秒1个单位的速度从原点O出发向右运动,同时,点M从点A出发以每秒7个单位的速度向左运动,点N从点B出发,以每秒10个单位的速度向右运动,P、Q分别为ME、ON的中点.思考:在运动过程中,
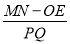 的值是否发生变化?请说明理由.
的值是否发生变化?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

-
科目: 来源: 题型:
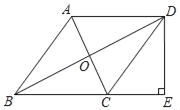
查看答案和解析>>【题目】如图,O为△ABC边AC的中点,AD∥BC交BO的延长线于点D,连接DC,DB平分∠ADC,作DE⊥BC,垂足为E.
(1)求证:四边形ABCD为菱形;
(2)若BD=8,AC=6,求DE的长.
相关试题

