【题目】直线y=kx+k﹣2经过点(m,n+1)和(m+1,2n+3),且﹣2<k<0,则n的取值范围是( )
A. ﹣2<n<0B. ﹣4<n<﹣2C. ﹣4<n<0D. 0<n<﹣2
参考答案:
【答案】B
【解析】
(方法一)根据一次函数图象上点的坐标特征可求出n=k﹣2,再结合k的取值范围,即可求出n的取值范围;
(方法二)利用一次函数k的几何意义,可得出k=n+2,再结合k的取值范围,即可求出n的取值范围.
解:(方法一)∵直线y=kx+k﹣2经过点(m,n+1)和(m+1,2n+3),
∴![]() ,
,
∴n=k﹣2.
又∵﹣2<k<0,
∴﹣4<n<﹣2.
(方法二)∵直线y=kx+k﹣2经过点(m,n+1)和(m+1,2n+3),
∴![]() .
.
∵﹣2<k<0,即﹣2<n+2<0,
∴﹣4<n<﹣2.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B在数轴上表示的数分别为﹣12和8,两只蚂蚁M、N分别从A、B两点同时匀速出发,同向而行
时间/秒
0
1
5
A点位置
﹣12
﹣9
B点位置
8
18
(1)请填写表格;
(2)若两只蚂蚁在数轴上点P相遇,求点P在数轴上表示的数;

(3)若运动t秒钟时,两只蚂蚁的距离为10,求出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知O为直线AD上一点,OB是∠AOC内部一条射线且满足∠AOB与∠AOC互补,OM,ON分别为∠AOC,∠AOB的平分线.

(1)∠COD与∠AOB相等吗?请说明理由;
(2)若∠AOB=30°,试求∠AOM与∠MON的度数;
(3)若∠MON=42°,试求∠AOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B在数轴上对应的数分别用+2、﹣6表示,P是数轴上的一个动点.

(1)数轴上A、B两点的距离为 .
(2)当P点满足PB=2PA时,求P点表示的数.
(3)将一枚棋子放在数轴上k0点,第一步从k点向右跳2个单位到k1,第二步从k1点向左跳4个单位到k2,第三步从k2点向右跳6个单位到k3,第四步从k3点向左跳8个单位到k4.
①如此跳6步,棋子落在数轴的k6点,若k6表示的数是12,则ko的值是多少?
②若如此跳了1002步,棋子落在数轴上的点k1002,如果k1002所表示的数是1998,那么k0所表示的数是 (请直接写答案).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校要从甲乙两名射击运动员中挑选一人参加全市比赛,在选拔赛中,每人进行了5次射击,甲的成绩(环)为:9.7,10,9.6,9.8,9.9;乙的成绩的平均数为9.8,方差为0.032;
(1)甲的射击成绩的平均数和方差分别是多少?
(2)据估计,如果成绩的平均数达到9.8环就可能夺得金牌,为了夺得金牌,应选谁参加比赛?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是中国电信两种“4G套餐”计费方式.(月基本费固定收,主叫不超过主叫时间,流量不超上网流量不再收取额外费用费,主叫超时和上网超流量部分加收超时费和超流量费)

(1)若某月小萱主叫通话时间为220分钟,上网流量为800 MB,则她按套餐1计费需 元,按套餐2计费需 元;若某月小花按套餐2计费需129元,主叫通话时间为240分钟,则上网流量为 MB.
(2)若上网流量为540 MB,是否存在某主叫通话时间t(分钟),按套餐1和套餐2的计费相等?若存在,请求出t的值;若不存在,请说明理由.
(3)上网流量为540 MB,直接写出当月主叫通话时间t(分钟)满足什么条件时,选择套餐1省钱?当每月主叫通话时间t(分钟)满足什么条件时,选择套餐2省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对数轴上的点
 进行如下操作:先把点
进行如下操作:先把点 表示的数乘以3,再把所得数对应的点向左平移1个单位,得到点
表示的数乘以3,再把所得数对应的点向左平移1个单位,得到点 的对应点
的对应点 .比如,点
.比如,点 表示3,3乘以3得9,表示9的点向左平移1个单位为8,因此点
表示3,3乘以3得9,表示9的点向左平移1个单位为8,因此点 的对应点
的对应点 表示的数为8.
表示的数为8.⑴点
 ,
, 在数轴上,对线段
在数轴上,对线段 上的每个点进行上述操作后得到线段
上的每个点进行上述操作后得到线段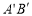 ,其中点
,其中点 ,
, 的对应点分别为
的对应点分别为 ,
, .如图,若点
.如图,若点 表示的数是1,则点
表示的数是1,则点 表示的数是__________;若点
表示的数是__________;若点 表示的数是
表示的数是 ,则点
,则点 表示的数是__________.
表示的数是__________.⑵若数轴上的点
 经过上述操作后,位置不变,则点
经过上述操作后,位置不变,则点 表示的数是__________.
表示的数是__________.
相关试题

