【题目】如图,在正方形ABCD中,连接AC,以点A为圆心,适当长为半径画弧,交AB、AC于点M,N,分别以M,N为圆心,大于MN长的一半为半径画弧,两弧交于点H,连结AH并延长交BC于点E,再分别以A、E为圆心,以大于AE长的一半为半径画弧,两弧交于点P,Q,作直线PQ,分别交CD,AC,AB于点F,G,L,交CB的延长线于点K,连接GE,下列结论:①∠LKB=22.5°,②GE∥AB,③tan∠CGF=![]() ,④S△CGE:S△CAB=1:4.其中正确的是( )
,④S△CGE:S△CAB=1:4.其中正确的是( )
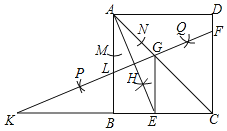
A. ①②③ B. ②③④ C. ①③④ D. ①②④
参考答案:
【答案】A
【解析】
①在△AOL和△BLK中,根据三角形内角和定理,如图两个角对应相等,则第三个角∠LKB=∠BAC=22.5°;
②根据线段中垂线定理证明∠AEG=∠EAG=22.5°=∠BAE,可得EG∥AB;
③根据等量代换可得:∠CGF=∠BLK,可作判断;
④连接EL,证明四边形ALEG是菱形,根据EL>BL,及相似三角形的性质可作判断.
①∵四边形ABCD是正方形,
∴∠BAC=![]() ∠BAD=45°,
∠BAD=45°,
由作图可知:AE平分∠BAC,
∴∠BAE=∠CAE=22.5°,
∵PQ是AE的中垂线,
∴AE⊥PQ,
∴∠AOL=90°,
∵∠AOL=∠LBK=90°,∠ALO=∠KLB,
∴∠LKB=∠BAE=22.5°;
故①正确;
②∵OG是AE的中垂线,
∴AG=EG,
∴∠AEG=∠EAG=22.5°=∠BAE,
∴EG∥AB,
故②正确;
③∵∠LAO=∠GAO,∠AOL=∠AOG=90°,
∴∠ALO=∠AGO,
∵∠CGF=∠AGO,∠BLK=∠ALO,
∴∠CGF=∠BLK,
在Rt△BKL中,tan∠CGF=tan∠BLK=![]() ,
,
故③正确;
④连接EL,
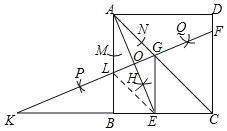
∵AL=AG=EG,EG∥AB,
∴四边形ALEG是菱形,
∴AL=EL=EG>BL,
∴![]() ,
,
∵EG∥AB,
∴△CEG∽△CBA,
∴![]() ,
,
故④不正确;
本题正确的是:①②③,
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:如图1、图2、图3,在
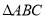 中,把
中,把 绕点
绕点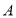 顺时针旋转
顺时针旋转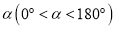 得到
得到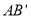 ,把
,把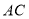 绕点
绕点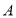 逆时针旋转
逆时针旋转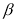 得到
得到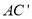 ,连接
,连接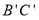 ,当
,当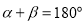 时,我们称
时,我们称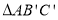 是
是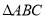 的“旋补三角形”,
的“旋补三角形”,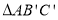 边
边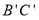 上的中线
上的中线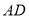 叫做
叫做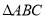 的“旋补中线”,点
的“旋补中线”,点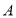 叫做“旋补中心”.图1、图2、图3中的
叫做“旋补中心”.图1、图2、图3中的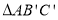 均是
均是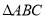 的“旋补三角形”.
的“旋补三角形”.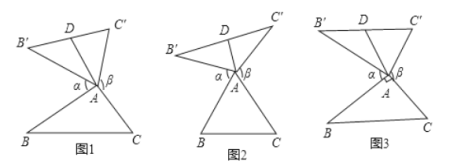
(1)①如图2,当
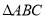 为等边三角形时,“旋补中线”
为等边三角形时,“旋补中线”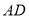 与
与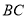 的数量关系为:
的数量关系为: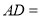 ______
______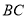 ;
;②如图3,当
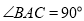 ,
,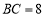 时,则“旋补中线”
时,则“旋补中线”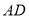 长为______.
长为______.(2)在图1中,当
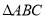 为任意三角形时,猜想“旋补中线”
为任意三角形时,猜想“旋补中线”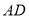 与
与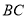 的数量关系,并给予证明.
的数量关系,并给予证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学兴趣小组的活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2
 的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.⑴小明发现DG⊥BE,请你帮他说明理由.
⑵如图②,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线与x轴交于A,B两点(点B在点A的右侧),且A,B两点的坐标分别为(-2,0),(8,0),与y轴交于点C(0,-4),连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线L交抛物线于点Q,交BD于点M.
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,试探究m为何值时,四边形CQMD是平行四边形?
(3)位于第四象限内的抛物线上是否存在点N,使得△BCN的面积最大?若存在,求出N点的坐标,及△BCN面积的最大值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】操作探究:
数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图1所示的长方形纸条ABCD,其中AD=BC=1,AB=CD=5.然后在纸条上任意画一条截线段MN,将纸片沿MN折叠,MB与DN交于点K,得到△MNK.如图2所示:

探究:
(1)若∠1=70°,∠MKN= °;
(2)改变折痕MN位置,△MNK始终是 三角形,请说明理由;
应用:
(3)爱动脑筋的小明在研究△MNK的面积时,发现KN边上的高始终是个不变的值.根据这一发现,他很快研究出△KMN的面积最小值为
 ,此时∠1的大小可以为 °
,此时∠1的大小可以为 °(4)小明继续动手操作,发现了△MNK面积的最大值.请你求出这个最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景介绍)勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
(小试牛刀)把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
S梯形ABCD= ,
S△EBC= ,
S四边形AECD= ,
则它们满足的关系式为 ,经化简,可得到勾股定理.
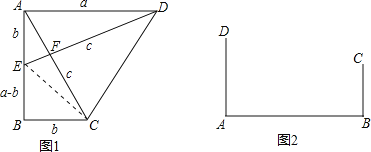
(知识运用)(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP的距离.
(知识迁移)借助上面的思考过程与几何模型,求代数式
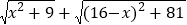 最小值(0<x<16)
最小值(0<x<16) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F是□ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.

(1)请写出图中全等三角形(不再添加辅助线).
(2)求证:△ABE≌△CDF;
相关试题

