【题目】我们定义:如图1、图2、图3,在![]() 中,把
中,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,当
,当![]() 时,我们称
时,我们称![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“旋补中线”,点
的“旋补中线”,点![]() 叫做“旋补中心”.图1、图2、图3中的
叫做“旋补中心”.图1、图2、图3中的![]() 均是
均是![]() 的“旋补三角形”.
的“旋补三角形”.
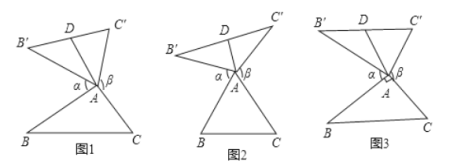
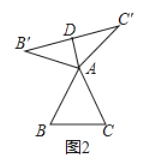
(1)①如图2,当![]() 为等边三角形时,“旋补中线”
为等边三角形时,“旋补中线”![]() 与
与![]() 的数量关系为:
的数量关系为:![]() ______
______![]() ;
;
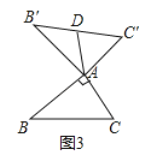
②如图3,当![]() ,
,![]() 时,则“旋补中线”
时,则“旋补中线”![]() 长为______.
长为______.
(2)在图1中,当![]() 为任意三角形时,猜想“旋补中线”
为任意三角形时,猜想“旋补中线”![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.
参考答案:
【答案】(1)①![]() ;②4;(2)结论:
;②4;(2)结论:![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)①首先证明△ADB'是含有30°的直角三角形,可得AD=![]() AB'即可解决问题;
AB'即可解决问题;
②首先证明△BAC≌△B'AC',根据直角三角形斜边中线等于斜边的一半即可解决问题;
(2)结论:AD=![]() BC.如图1中,延长AD到M,使得AD=DM,连接B'M,C'M,首先证明四边形AC'MB'是平行四边形,再证明△BAC≌△AB'M,即可解决问题;
BC.如图1中,延长AD到M,使得AD=DM,连接B'M,C'M,首先证明四边形AC'MB'是平行四边形,再证明△BAC≌△AB'M,即可解决问题;
(1)①如图2中,
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为![]() .
.
②如图3中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
故答案为4.
(2)结论:![]() .
.
理由:如图1中,延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】现场学习题:
问题背景:
在△ABC中,AB、BC、AC三边的长分别为
 、
、 、
、 ,求这个三角形的面积.
,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.

(1)请你将△ABC的面积直接填写在横线上. .
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法,若△ABC三边的长分别为
 a,2
a,2 a、
a、 a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: .
a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: .探索创新:
(3)若△ABC三边的长分别为
 、
、 、
、 (m>0,n>0,m≠n),请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为: .
(m>0,n>0,m≠n),请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为: . -
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b,c是△ABC的三条边,关于x的方程
 x2+
x2+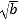 x+c-
x+c- a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.(1)试判断△ABC的形状;
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
-
科目: 来源: 题型:
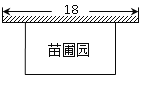
查看答案和解析>>【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学兴趣小组的活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2
 的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.⑴小明发现DG⊥BE,请你帮他说明理由.
⑵如图②,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线与x轴交于A,B两点(点B在点A的右侧),且A,B两点的坐标分别为(-2,0),(8,0),与y轴交于点C(0,-4),连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线L交抛物线于点Q,交BD于点M.
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,试探究m为何值时,四边形CQMD是平行四边形?
(3)位于第四象限内的抛物线上是否存在点N,使得△BCN的面积最大?若存在,求出N点的坐标,及△BCN面积的最大值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,连接AC,以点A为圆心,适当长为半径画弧,交AB、AC于点M,N,分别以M,N为圆心,大于MN长的一半为半径画弧,两弧交于点H,连结AH并延长交BC于点E,再分别以A、E为圆心,以大于AE长的一半为半径画弧,两弧交于点P,Q,作直线PQ,分别交CD,AC,AB于点F,G,L,交CB的延长线于点K,连接GE,下列结论:①∠LKB=22.5°,②GE∥AB,③tan∠CGF=
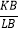 ,④S△CGE:S△CAB=1:4.其中正确的是( )
,④S△CGE:S△CAB=1:4.其中正确的是( )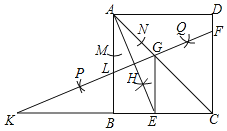
A. ①②③ B. ②③④ C. ①③④ D. ①②④
相关试题

