【题目】在数学兴趣小组的活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
⑴小明发现DG⊥BE,请你帮他说明理由.
⑵如图②,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.

参考答案:
【答案】(1)见解析 (2)![]()
【解析】(1)延长EB交DG于点H,先证出Rt△ADG≌Rt△ABE,得出∠AGD=∠AEB,﹢根据∠HBG=∠EBA,得出∠HGB+∠HBG=90°即可;
(2)过点A作AP⊥BD交BD于点P,根据△DAG≌△BAE得出DG=BE,∠APD=90°,求出AP、DP,利用勾股定理求出PG,﹢根据DG=DP+PG求出DG,最后根据DG=BE即可得出答案.
解:(1)如解图①所示,延长EB交DG于点H.
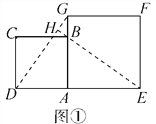
∵四边形ABCD和四边形AEFG都为正方形,
∴AD=AB,∠DAG=∠BAE=90°,AG=AE,
∴△ADG≌△ABE(SAS), ∴∠AGD=∠AEB.
在△ADG中,∠AGD+∠ADG=90°,
∴∠AEB+∠ADG=90°.
在△EDH中,∠AEB+∠ADG+∠DHE=180°,
∴∠DHE=90°,即DG⊥BE
(2)如解图②,连结DG,过点A作AM⊥DG交DG于点M,
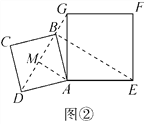
∠AMD=∠AMG=90°.
∵四边形ABCD和四边形AEFG都为正方形,
∴AD=AB,∠DAB=∠GAE=90°,AG=AE,
∴∠DAB+∠BAG=∠GAE+∠BAG,即∠DAG=∠BAE.
在△ADG和△ABE中,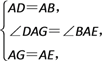
∴△ADG≌△ABE(SAS),∴DG=BE.
∵BD为正方形ABCD的对角线,∴∠MDA=45°.
在Rt△AMD中,∠MDA=45°,
∵AD=2,∴DM=AM=![]() ,
,
在Rt△AMG中,根据勾股定理得:
GM=![]() =
=![]() .
.
∵DG=DM+GM=![]() +
+![]() ,
,
∴BE=DG=![]() +
+![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=
 ,b=
,b= ,c=
,c= ②a=6,∠A=45°; ③∠A=32°,∠B=58°;
②a=6,∠A=45°; ③∠A=32°,∠B=58°; ④a=7,b=24,c=25 ⑤a=2,b=2,c=4.
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红家最近新盖了房子,室内装修时,木工师傅让小红爸爸去建材市场买一块长3m,宽2.2m的薄木板用来做家居面,到了市场爸爸看到满足这个尺寸的木板有点大,买还是不买爸爸犹豫了,因为他知道他家门框高只有2m,宽只有1m,他不知道这块木板买回家后能不能完整的通过自家门框.请你替小红爸爸解决一下难题,帮他算一算要买的木板能否通过自家门框进入室内.(备用图可供做题参考,薄木板厚度可以忽略不计)

-
科目: 来源: 题型:
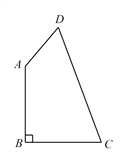
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
(1)求∠DAB的度数.
(2)求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣
 x2﹣
x2﹣ x+2与x轴交于A、B两点,与y轴交于点C.
x+2与x轴交于A、B两点,与y轴交于点C.⑴求点A,B,C的坐标;
⑵点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
⑶此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC 中,∠C=90°,BC=3,AC=4.现在要将交ABC 扩充成等腰三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后等腰三角形的周长.
赵佳同学是这样操作的:如图 1 所示,延长BC 到点 D,使CD=BC,连接AD.所以,△ADB 为符合条件的三角形.则此时△ADB的周长为____________.
请你在图2、图3中再设计两种扩充方案,并直接写出扩充后等腰三角形的周长.
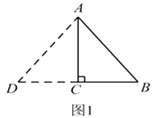
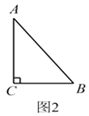
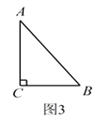
图2的周长:______________;图3的周长:______________.
相关试题

