【题目】操作探究:
数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图1所示的长方形纸条ABCD,其中AD=BC=1,AB=CD=5.然后在纸条上任意画一条截线段MN,将纸片沿MN折叠,MB与DN交于点K,得到△MNK.如图2所示:

探究:
(1)若∠1=70°,∠MKN= °;
(2)改变折痕MN位置,△MNK始终是 三角形,请说明理由;
应用:
(3)爱动脑筋的小明在研究△MNK的面积时,发现KN边上的高始终是个不变的值.根据这一发现,他很快研究出△KMN的面积最小值为![]() ,此时∠1的大小可以为 °
,此时∠1的大小可以为 °
(4)小明继续动手操作,发现了△MNK面积的最大值.请你求出这个最大值.

参考答案:
【答案】(1)、40;(2)、等腰;(3)、45°或135°(4)、最大值为1.3.
【解析】
试题分析:(1)、根据矩形的性质和折叠的性质求出∠KNM,∠KMN的度数,根据三角形内角和即可求解;
(2)、利用翻折变换的性质以及两直线平行内错角相等得出KM=KN;(3)、利用当△KMN的面积最小值为![]() 时,KN=BC=1,故KN⊥B′M,得出∠1=∠NMB=45°,同理当将纸条向下折叠时,∠1=∠NMB=135°;(4)、分情况一:将矩形纸片对折,使点B与D重合,此时点K也与D重合;情况二:将矩形纸片沿对角线AC对折,此时折痕即为AC两种情况讨论求解.
时,KN=BC=1,故KN⊥B′M,得出∠1=∠NMB=45°,同理当将纸条向下折叠时,∠1=∠NMB=135°;(4)、分情况一:将矩形纸片对折,使点B与D重合,此时点K也与D重合;情况二:将矩形纸片沿对角线AC对折,此时折痕即为AC两种情况讨论求解.
试题解析:(1)、如图1, ∵四边形ABCD是矩形, ∴AM∥DN. ∴∠KNM=∠1. ∵∠1=70°,
∴∠KNM=∠KMN=∠1=70°, ∴∠MKN=40°.
(2)、等腰, 理由:∵AB∥CD,∴∠1=∠MND, ∵将纸片沿MN折叠, BGFYTTTQ ∴∠1=∠KMN,∠MND=∠KMN,
∴KM=KN;
(3)、如图2,当△KMN的面积最小值为![]() 时,KN=BC=1,故KN⊥B′M, ∵∠NMB=∠KMN,∠KMB=90°,
时,KN=BC=1,故KN⊥B′M, ∵∠NMB=∠KMN,∠KMB=90°,
∴∠1=∠NMB=45°,同理当将纸条向下折叠时,∠1=∠NMB=135°,
(4)、分两种情况:
情况一:如图3,将矩形纸片对折,使点B与D重合,此时点K也与D重合. MK=MB=x,则AM=5﹣x.
由勾股定理得12+(5﹣x)2=x2, 解得x=2.6. ∴MD=ND=2.6. S△MNK=S△MND=![]() ×1×2.6=1.3.
×1×2.6=1.3.
情况二:如图4,将矩形纸片沿对角线AC对折,此时折痕即为AC. MK=AK=CK=x,则DK=5﹣x.
同理可得MK=NK=2.6. ∵MD=1, ∴S△MNK=![]() ×1×2.6=1.3. △MNK的面积最大值为1.3.
×1×2.6=1.3. △MNK的面积最大值为1.3.




-
科目: 来源: 题型:
查看答案和解析>>【题目】请把命题“有两个角相等的三角形是等腰三角形”改写成“如果…,那么…”的表述形式: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,己知A(﹣1,5),B(4,2),C(﹣1,0)三点.
(1)点A关于原点O的对称点A′的坐标为 ,点B关于x轴的对称点B′的坐标为 ,点C关于y轴的对称点C′的坐标为 .
(2)在图中画出△A′B′C′,并求它的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中A(-2,3),B(-3,1),C(-1,2)
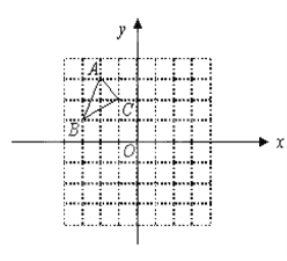
(1)画出△ABC关于
 轴、y轴对称的△A1B1C1和△A2B2C2;
轴、y轴对称的△A1B1C1和△A2B2C2;(2)将△ABC绕原点O旋转1800,画出旋转后的△A3B3C3;
(3)在△A1B1C1,△A2B2C2,△A3B3C3中, 与 成轴对称,对称轴是 ;(填一组即可) 与 成中心对称,对称中心的坐标是
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角互补的平行四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直且相等的四边形是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.每一个命题都有逆命题B.每一个定理都有逆定理
C.真命题的逆命题一定是真命题D.真命题的逆命题一定是假命题
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x2+y2)(x2+y2﹣1)=12,则x2+y2= .
相关试题

