【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是 . (写出正确命题的序号) 
参考答案:
【答案】①④
【解析】解:由二次函数图象开口向上,得到a>0;与y轴交于负半轴,得到c<0, ∵对称轴在y轴右侧,且﹣ ![]() =1,即2a+b=0,
=1,即2a+b=0,
∴a与b异号,即b<0,
∴abc>0,选项①正确;
∵二次函数图象与x轴有两个交点,
∴△=b2﹣4ac>0,即b2>4ac,选项②错误;
∵原点O与对称轴的对应点为(2,0),
∴x=2时,y<0,即4a+2b+c<0,选项③错误;
∵x=﹣1时,y>0,
∴a﹣b+c>0,
把b=﹣2a代入得:3a+c>0,选项④正确,
故答案是:①④.
根据抛物线开口方向,对称轴的位置,与x轴交点个数,以及x=﹣1,x=2对应y值的正负判断即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长分别为2和4的两个全等三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止,设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )
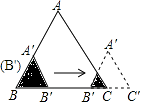
A.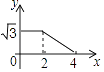
B.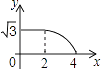
C.
D.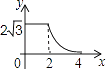
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△
 中,
中, >
> ,
, ∥
∥ =
= ,点
,点 在
在 边上,连接
边上,连接 ,则添加下列哪一个条件后,仍无法判定△
,则添加下列哪一个条件后,仍无法判定△ 与△
与△ 全等( )
全等( )
A.
 ∥
∥ B.
B.  C. ∠
C. ∠ =∠
=∠ D. ∠
D. ∠ =∠
=∠
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果△ABC和△DEF这两个三角形全等,点C和点E,点B和点D分别是对应点,则另一组对应点是________,对应边是______________,对应角是_____________,表示这两个三角形全等的式子是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△EFG≌△NMH, ∠F与∠M是对应角.

(1)写出相等的线段与相等的角;
(2)若EF=2.1cm,FH=1.1cm,HM=3.3cm,求MN和HG的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(﹣1,m)和点B(n,5).

(1)求该二次函数的关系式;
(2)在给定的平面直角坐标系中,画出这两个函数的大致图象;
(3)结合图象直接写出x2+bx+c>x+1时x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣(2m+1)+(
 m2﹣1).
m2﹣1).
(1)求证:不论m取什么实数,该二次函数图象与x轴总有两个交点;
(2)若该二次函数图象经过点(2m﹣2,﹣2m﹣1),求该二次函数的表达式.
相关试题

