【题目】如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线![]() 的一支在第一象限交梯形对角线OC于点D,交边BC于点E.(1)填空:双曲线的另一支在第_____象限,k的取值范围是_____;
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.(1)填空:双曲线的另一支在第_____象限,k的取值范围是_____;
(2)若点C的坐标为(2,2),当点E在什么位置时?阴影部分面积S最小?
(3)若![]() ,
, ![]() =2,求双曲线的解析式.
=2,求双曲线的解析式.

参考答案:
【答案】(1) 三,k>0 (2) 当点E在BC的中点时,阴影部分的面积S最小 (3) y=![]()
【解析】【试题分析】
(1)根据双曲线的性质,k>0,双曲线在一、三象限;k<0,在二、四象限.根据题意,该双曲线的另一支一定在第三象限,且k>0;
(2)由题意得:A点的纵坐标为2,E点的横坐标为2,根据反比例函数![]() ,设A点的坐标为(
,设A点的坐标为(![]() ,2),E点的坐标为(2,
,2),E点的坐标为(2, ![]() ),则阴影部分的面积为
),则阴影部分的面积为
S△ACE+S△OBE=![]() ×(2-
×(2-![]() )×(2-
)×(2-![]() )+
)+![]() ×2×
×2×![]() =
=![]()
![]() +
+![]() ,当k-2=0,即k=2时,
,当k-2=0,即k=2时, ![]() 最小,最小值为
最小,最小值为![]() ;即E点的坐标为(2,1),即E点为BC的中点.
;即E点的坐标为(2,1),即E点为BC的中点.
(3)设D点坐标为(a, ![]() ),根据中点坐标公式得C点坐标为(2a,
),根据中点坐标公式得C点坐标为(2a, ![]() ), 则A点的纵坐标为
), 则A点的纵坐标为![]() ,代入y=
,代入y=![]() 得,x=
得,x=![]() ,得A点坐标为(
,得A点坐标为(![]() ,
,![]() ),根据
),根据![]() =2,得
=2,得![]() ×(2a-
×(2a-![]() )×
)×![]() =2,解得k=
=2,解得k=![]() ,
,
【试题解析】
(1)三,k>0;
(2)∵梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,
而点C的坐标为(2,2),
∴A点的纵坐标为2,E点的横坐标为2,B点坐标为(2,0),把y=2代入y=![]() ,得,x=
,得,x=![]() ,
,
把x=2代入y=![]() 得,y=
得,y=![]() ,
,
∴A点的坐标为(![]() ,2),
,2),
E点的坐标为(2, ![]() ),
),
∴![]() =S△ACE+S△OBE,
=S△ACE+S△OBE,
=![]() ×(2-
×(2-![]() )×(2-
)×(2-![]() )+
)+![]() ×2×
×2×![]() ,
,
=![]()
![]() +
+![]() ,
,
当k-2=0,即k=2时, ![]() 最小,最小值为
最小,最小值为![]() ;
;
∴E点的坐标为(2,1),即E点为BC的中点,
∴当点E在BC的中点时,阴影部分的面积S最小;
(3)设D点坐标为(a, ![]() ),
),
∵![]() =
=![]() ,
,
∴2OD=OC,
即D点为OC的中点,
∴C点坐标为(2a, ![]() ),
),
∴A点的纵坐标为![]() ,
,
把y=![]() 代入y=
代入y=![]() 得,x=
得,x=![]() ,
,
∴A点坐标为(![]() ,
,![]() )
)
∵![]() =2,
=2,
∴![]() ×(2a-
×(2a-![]() )×
)×![]() =2,
=2,
∴k=![]() ,
,
∴双曲线的解析式为y=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的不等式x﹣k≤0的正整数解是1、2、3,那么k的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次数学课外实践活动中,要求测教学楼的高度AB.小刚在D处用高1.5m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40m到达E,又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是16的算术平方根,b是﹣27的立方根,求a3+b2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一食堂需要购买盒子存放食物,盒子有A、B两种型号,单个盒子的容量和价格如表格所示.现有15升食物需要存放且要求每个盒子都要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性每个返还现金1.5元,则该食堂购买盒子所需最少费用是__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】宁波某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共10台,具体情况如下表:
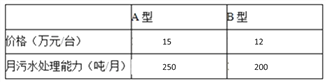
经预算,企业最多支出136万元购买设备,且要求月处理污水能力不低于2150吨.
(1)该企业有哪几种购买方案?
(2)哪种方案更省钱?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 (其中
(其中 )与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.(1)求抛物线的关系式;
(2)过点
 的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标. 
相关试题

