搜索
【题目】如图，已知抛物线
（其中
）与x轴交于点A、B（点A在点B的左侧），与y轴交于点C，抛物线的对称轴l与x轴交于点D，且点D恰好在线段BC的垂直平分线上．
（1）求抛物线的关系式；
（2）过点
的线段MN∥y轴，与BC交于点P，与抛物线交于点N．若点E是直线l上一点，且∠BED＝∠MNB－∠ACO时，求点E的坐标．
参考答案：
【答案】（1）抛物线的关系式为
；
（2）点E的坐标为
或
【解析】试题分析：(1)由题意可求得点
、
、
试题解析：
（1）求得点
、
、
易得∠ACB＝90°，由△AOC∽△COB可得
∴
（2）易证∠ACO＝∠CBO，∠MNB＝∠MBN，所以∠BED＝∠CBN
连结CN， 由勾股定理得CN＝
，BC＝
，BN＝
， 由勾股定理逆定理证得∠CNB＝90°，从而得
然后解Rt△BED可得DE＝
，
∴点E坐标为
或
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列光线所形成投影是平行投影的是（ ）
A. 太阳光线B. 台灯的光线
C. 手电筒的光线D. 路灯的光线
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，O为直线AB上一点，∠AOC＝50°，OD平分∠AOC，∠DOE＝90°.
(1)请你数一数，图中有多少个小于平角的角；
(2)求出∠BOD的度数；
(3)请通过计算说明OE是否平分∠BOC.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB与CD相交于点O，OD平分∠BOE，∠FOD=90°，问OF是∠AOE的平分线吗？请你补充完整小红的解答过程．
探究：
（1）当∠BOE=70°时，
∠BOD=∠DOE=
，∠EOF=90°﹣∠DOE= °，
而∠AOF+∠FOD+∠BOD=180°，
所以∠AOF+∠BOD=180°﹣∠FOD=90°，
所以∠AOF=90°﹣∠BOD= °，
所以∠EOF=∠AOF，OF是∠AOE的平分线．
（2）参考上面（1）的解答过程，请你证明，当∠BOE为任意角度时，OF是∠AOE的平分线．
（3）直接写出与∠AOF互余的所有角．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各对数中，互为相反数的是（ ）
A. ﹣（+3）与+（﹣3）B. ﹣（﹣4）与|﹣4|
C. ﹣32与（﹣3）2D. ﹣23与（﹣2）3
-
科目： 来源： 题型：
查看答案和解析>>【题目】“夕阳红”养老院共有普通床位和高档床位共500张．已知今年一月份入住普通床位老人300人，入住高档床位老人90人，共计收费51万元；今年二月份入住普通床位老人350人，入住高档床位老人100人，共计收费58万元．
（1）求普通床位和高档床位每月收费各多少元？
（2）根据国家养老政策规定，为保障普通居民的养老权益，所有实际入住高档床位数不得超过实际入住普通床位数的三分之一；另外为扶持养老企业发展国家民政局财政对每张入住的床位平均每年都是给予养老院企业2400元的补贴．经测算，该养老院普通床位的运营成本是每月1200元/张，入住率为90%；高档床位的运营成本是每月2000元/张，入住率为70%．问该养老院应该怎样安排500张床的普通床位和高档床位数量，才能使每月的利润最大，最大为多少元？（月利润=月收费-月成本+月补贴）
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下两幅统计图．请根据相关信息，解答下列问题：
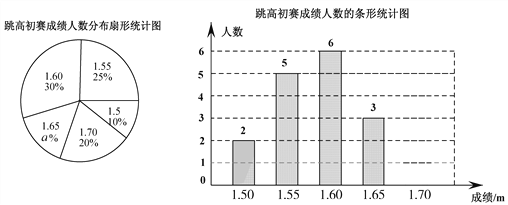
（1）扇形统计图中，初赛成绩为1.65m所在扇形图形的圆心角为_ _°；
（2）补全条形统计图；
（3）这组初赛成绩的中位数是 m；
（4）根据这组初赛成绩确定8人进入复赛，那么初赛成绩为1.60m的运动员杨强能否进入复赛？为什么？
相关试题
