【题目】宁波某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共10台,具体情况如下表:
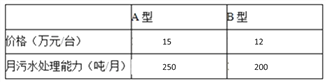
经预算,企业最多支出136万元购买设备,且要求月处理污水能力不低于2150吨.
(1)该企业有哪几种购买方案?
(2)哪种方案更省钱?并说明理由.
参考答案:
【答案】(1)见解析;(2)购买3台A型污水处理设备,7台B型污水处理设备更省钱.
【解析】试题分析:(1)设购买污水处理设备A型号x台,则购买B型号(10-x)台,根据企业最多支出136万元购买设备,要求月处理污水能力不低于2150吨,列出不等式组,然后找出最合适的方案即可.
(2)计算出每一方案的花费,通过比较即可得到答案.
试题解析:(1)设购买污水处理设备A型号x台,则购买B型号(10-x)台,
根据题意,得
![]()
解这个不等式组,得:![]()
∵x是整数
∴x=3或x=4或x=5.
当x=3时,10-x=7;
当x=4时,10-x=6;
当x=5时,10-x=5.
答:有3种购买方案:第一种是购买3台A型污水处理设备,7台B型污水处理设备.第二种是购买4台A型污水处理设备,6台B型污水处理设备;第三种是购买5台A型污水处理设备,5台B型污水处理设备.
(2)当x=3时,购买资金为15×3+12×7=129(万元),
当x=4时,购买资金为15×4+12×6=132(万元),
当x=5时,购买资金为15×5+12×5=135(万元).
因为135>132>129,所以为了节约资金,应购污水处理设备A型号3台,B型号7台.
(用一次函数y=3x+120增减性说明也可以)
答:购买3台A型污水处理设备,7台B型污水处理设备更省钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是16的算术平方根,b是﹣27的立方根,求a3+b2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线
 的一支在第一象限交梯形对角线OC于点D,交边BC于点E.(1)填空:双曲线的另一支在第_____象限,k的取值范围是_____;
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.(1)填空:双曲线的另一支在第_____象限,k的取值范围是_____;(2)若点C的坐标为(2,2),当点E在什么位置时?阴影部分面积S最小?
(3)若
 ,
,  =2,求双曲线的解析式.
=2,求双曲线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一食堂需要购买盒子存放食物,盒子有A、B两种型号,单个盒子的容量和价格如表格所示.现有15升食物需要存放且要求每个盒子都要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性每个返还现金1.5元,则该食堂购买盒子所需最少费用是__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 (其中
(其中 )与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.(1)求抛物线的关系式;
(2)过点
 的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】“夕阳红”养老院共有普通床位和高档床位共500张.已知今年一月份入住普通床位老人300人,入住高档床位老人90人,共计收费51万元;今年二月份入住普通床位老人350人,入住高档床位老人100人,共计收费58万元.
(1)求普通床位和高档床位每月收费各多少元?
(2)根据国家养老政策规定,为保障普通居民的养老权益,所有实际入住高档床位数不得超过实际入住普通床位数的三分之一;另外为扶持养老企业发展国家民政局财政对每张入住的床位平均每年都是给予养老院企业2400元的补贴.经测算,该养老院普通床位的运营成本是每月1200元/张,入住率为90%;高档床位的运营成本是每月2000元/张,入住率为70%.问该养老院应该怎样安排500张床的普通床位和高档床位数量,才能使每月的利润最大,最大为多少元?(月利润=月收费-月成本+月补贴)
-
科目: 来源: 题型:
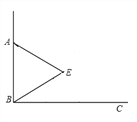
查看答案和解析>>【题目】如图,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连接AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连接QE并延长交射线BC于点F.
(1)如图,当BP=BA时,∠EBF=______°,猜想∠QFC =______°;
(2)如图,当点P为射线BC上任意一点时,猜想∠QFC的度数,并加以证明.
(3)已知线段AB=
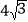 ,设BP=x,点Q到射线BC的距离为y,求y关于x的函数关系式.
,设BP=x,点Q到射线BC的距离为y,求y关于x的函数关系式.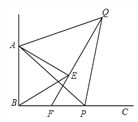
相关试题

