【题目】证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
(1)已知:如图,∠AOC=∠BOC,点P在OC上,________
求证:________.
请你补全已知和求证
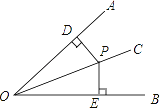
(2)并写出证明过程.
参考答案:
【答案】(1)PD⊥OA,PE⊥OB;PD=PE(2)PD=PE
【解析】
(1)根据图形写出已知条件和求证即可;
(2)利用全等三角形的判定得出△PDO≌△PEO,由全等三角形的性质可得结论.
(1)PD⊥OA,PE⊥OB;PD=PE
(2)解:已知:PD⊥OA,PE⊥OB,垂足分别为D,E;求证:PD=PE.
∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°,
在△PDO和△PEO中,

∴△PDO≌△PEO(AAS),
∴PD=PE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,对角线AC、BD交于点O(如图),则图中全等三角形的对数为( )
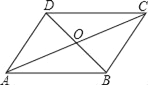
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.
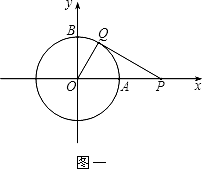
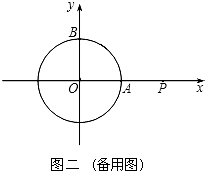
(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是⊙O的切线,连接OQ.求∠QOP的大小;
(2)若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被⊙O截得的弦长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣
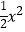 +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).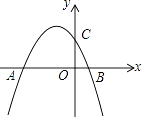
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于圆O,∠BAD=90°,AC为直径,过点A作圆O的切线交CB的延长线于点E,过AC的三等分点F(靠近点C)作CE的平行线交AB于点G,连结CG.

(1)求证:AB=CD;
(2)求证:CD2=BEBC;
(3)当CG=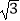 ,BE=
,BE=  时,求CD的长.
时,求CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=∠ABC,DE垂直平分BC,交BC于点D,交AC于点E.

(1)若AB=5,BC=8,求△ABE的周长;
(2)若BE=BA,求∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(时)之间的关系的图象如图所示.根据图中提供的信息,有下列说法:①他们都行驶了18千米;②甲在中途停留了0.5小时;③乙比甲晚出发了0.5小时;④甲、乙两人同时到达目的地;⑤乙追上甲后甲的速度<乙的速度.其中符合图象描述的说法有( )
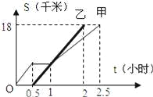
A. 2个 B. 3个 C. 4个 D. 5个
相关试题

