【题目】如图,抛物线y=﹣ ![]() x2+bx+c过点A(4,0),B(﹣4,﹣4).
x2+bx+c过点A(4,0),B(﹣4,﹣4). 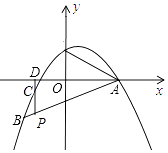
(1)求抛物线的解析式;
(2)若点P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交抛物线及x轴于C、D两点.请问是否存在这样的点P,使PD=2CD?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:由题意 ![]() ,解得
,解得 ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)解:∵A(4,0),B(﹣4,﹣4),
∴直线AB的解析式为y= ![]() x﹣2,
x﹣2,
设P(m, ![]() m﹣2),其中﹣4<m<4,则C(m,﹣
m﹣2),其中﹣4<m<4,则C(m,﹣ ![]() m2+
m2+ ![]() m+2),PD=2﹣
m+2),PD=2﹣ ![]() m,CD=|﹣
m,CD=|﹣ ![]() m2+
m2+ ![]() m+2|,
m+2|,
① 当点C在x轴上方时,CD=﹣ ![]() m2+
m2+ ![]() m+2,由PD=2CD,
m+2,由PD=2CD,
得2﹣ ![]() m=2(﹣
m=2(﹣ ![]() m2+
m2+ ![]() m+2),解得m=﹣1或4(舍弃),
m+2),解得m=﹣1或4(舍弃),
∴P(﹣1,﹣ ![]() ).
).
②当点C在x轴下方时,CD= ![]() m2﹣
m2﹣ ![]() m﹣2,由PD=2CD,得2﹣
m﹣2,由PD=2CD,得2﹣ ![]() m=2(
m=2( ![]() m2﹣
m2﹣ ![]() m﹣2),解得m=﹣3或4(舍弃),
m﹣2),解得m=﹣3或4(舍弃),
∴P(﹣3,﹣ ![]() ),
),
综上所述,点P的坐标为(﹣1,﹣ ![]() )或(﹣3,﹣
)或(﹣3,﹣ ![]() )
)
【解析】(1)利用待定系数法把问题转化为方程组解决.(2)设P(m, ![]() m﹣2),其中﹣4<m<4,则C(m,﹣
m﹣2),其中﹣4<m<4,则C(m,﹣ ![]() m2+
m2+ ![]() m+2),PD=2﹣
m+2),PD=2﹣ ![]() m,CD=|﹣
m,CD=|﹣ ![]() m2+
m2+ ![]() m+2|,分两种情形①当点C在x轴上方时,CD=﹣
m+2|,分两种情形①当点C在x轴上方时,CD=﹣ ![]() m2+
m2+ ![]() m+2,由PD=2CD,得2﹣
m+2,由PD=2CD,得2﹣ ![]() m=2(﹣
m=2(﹣ ![]() m2+
m2+ ![]() m+2),②当点C在x轴下方时,CD=
m+2),②当点C在x轴下方时,CD= ![]() m2﹣
m2﹣ ![]() m﹣2,由PD=2CD,列出方程即可解决问题.
m﹣2,由PD=2CD,列出方程即可解决问题.
【考点精析】关于本题考查的二次函数的图象,需要了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB是⊙O的直径,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.

(1)求证:∠PCA=∠B;
(2)填空:已知∠P=40°,AB=12cm,点Q在 上,从点A开始以πcm/s的速度逆时针运动到点C停止,设运动时间为ts. ①当t=时,以点A、Q、B、C为顶点的四边形面积最大;
上,从点A开始以πcm/s的速度逆时针运动到点C停止,设运动时间为ts. ①当t=时,以点A、Q、B、C为顶点的四边形面积最大;
②当t=时,四边形AQBC是矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,矩形ABCD中,AB=2,BC=5,BP=1,∠MPN=90°,将∠MPN绕点P从PB处开始按顺时针方向旋转,PM交边AB(或AD)于点E,PN交边AD(或CD)于点F,当PN旋转至PC处时,∠MPN的旋转随即停止.
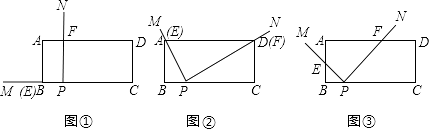
(1)特殊情形:如图②,发现当PM过点A时,PN也恰巧过点D,此时,△ABP△PCD(填“≌”或“~”);
(2)类比探究:如图③,在旋转过程中,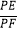 的值是否为定值?若是,请求出该定值;若不是,请说明理由.
的值是否为定值?若是,请求出该定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角△ABC中,边BC长为12,高AD长为8.
(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.
①求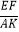 的值;
的值;
②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值;
(2)若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c交x轴于A(﹣1,0)、B两点,交y轴于点C(0,5),且过点D(1,8),M为其顶点.
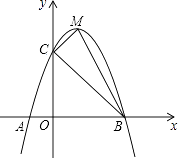
(1)求抛物线的解析式;
(2)求△MCB的面积;
(3)在抛物线上是否存在点P,使△PAB的面积等于△MCB的面积?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=15,AC=12,BC=9,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是( )

A.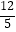
B.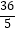
C.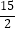
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,其对称轴方程为x=﹣1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a﹣b+c<0,则正确的结论是( )
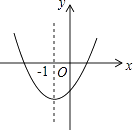
A.①②③④
B.②④⑤
C.①④⑤
D.②③④
相关试题

