【题目】如图,抛物线y=ax2+bx+c交x轴于A(﹣1,0)、B两点,交y轴于点C(0,5),且过点D(1,8),M为其顶点. 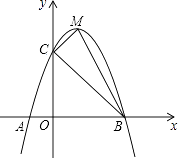
(1)求抛物线的解析式;
(2)求△MCB的面积;
(3)在抛物线上是否存在点P,使△PAB的面积等于△MCB的面积?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵A(﹣1,0),C(0,5),D(1,8)三点在抛物线y=ax2+bx+c上,
∴ 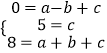 ,
,
解方程组,得 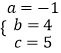 ,
,
故抛物线的解析式为y=﹣x2+4x+5
(2)解:过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积= ![]() MNOB.
MNOB.
∵y=﹣x2+4x+5=﹣(x﹣5)(x+1)=﹣(x﹣2)2+9,
∴M(2,9),B(5,0),
由B、C两点的坐标易求得直线BC的解析式为:y=﹣x+5,
当x=2时,y=﹣2+5=3,则N(2,3),
则MN=9﹣3=6,
则S△MCB= ![]() ×6×5=15
×6×5=15
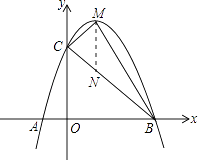
(3)解:在抛物线上存在点P,使△PAB的面积等于△MCB的面积.理由如下:
∵A(﹣1,0),B(5,0),
∴AB=6,
∵△PAB的面积=△MCB的面积,
∴ ![]() ×6×|yP|=15,
×6×|yP|=15,
∴|yP|=5,yP=±5.
当yP=5时,﹣x2+4x+5=5,解得x1=0,x2=4;
当yP=﹣5时,﹣x2+4x+5=﹣5,解得x3=2+ ![]() ,x4=2﹣
,x4=2﹣ ![]() .
.
故在抛物线上存在点P1(0,5),P2(4,5),P3(2+ ![]() ,﹣5),P3(2﹣
,﹣5),P3(2﹣ ![]() ,﹣5),使△PAB的面积等于△MCB的面积.
,﹣5),使△PAB的面积等于△MCB的面积.
【解析】(1)由A、C、D三点在抛物线上,根据待定系数法即可求出抛物线的解析式;(2)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积= ![]() MNOB;(3)先由△PAB的面积等于△MCB的面积,求出AB边上的高即点P的纵坐标的绝对值,再将点P的纵坐标代入抛物线的解析式,得到一元二次方程,如果方程有实数根,则在抛物线上存在点P,否则不存在.
MNOB;(3)先由△PAB的面积等于△MCB的面积,求出AB边上的高即点P的纵坐标的绝对值,再将点P的纵坐标代入抛物线的解析式,得到一元二次方程,如果方程有实数根,则在抛物线上存在点P,否则不存在.
【考点精析】认真审题,首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,矩形ABCD中,AB=2,BC=5,BP=1,∠MPN=90°,将∠MPN绕点P从PB处开始按顺时针方向旋转,PM交边AB(或AD)于点E,PN交边AD(或CD)于点F,当PN旋转至PC处时,∠MPN的旋转随即停止.
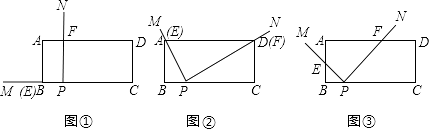
(1)特殊情形:如图②,发现当PM过点A时,PN也恰巧过点D,此时,△ABP△PCD(填“≌”或“~”);
(2)类比探究:如图③,在旋转过程中,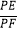 的值是否为定值?若是,请求出该定值;若不是,请说明理由.
的值是否为定值?若是,请求出该定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角△ABC中,边BC长为12,高AD长为8.
(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.
①求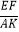 的值;
的值;
②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值;
(2)若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+bx+c过点A(4,0),B(﹣4,﹣4).
x2+bx+c过点A(4,0),B(﹣4,﹣4). 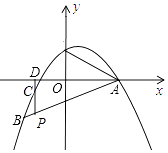
(1)求抛物线的解析式;
(2)若点P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交抛物线及x轴于C、D两点.请问是否存在这样的点P,使PD=2CD?若存在,请求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=15,AC=12,BC=9,经过点C且与边AB相切的动圆与CB、CA分别相交于点E、F,则线段EF长度的最小值是( )

A.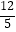
B.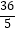
C.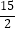
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,其对称轴方程为x=﹣1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a﹣b+c<0,则正确的结论是( )
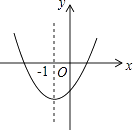
A.①②③④
B.②④⑤
C.①④⑤
D.②③④ -
科目: 来源: 题型:
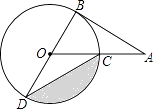
查看答案和解析>>【题目】如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为(结果保留π)
相关试题

