【题目】如图,在⊙O中,AB是⊙O的直径,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC. 
(1)求证:∠PCA=∠B;
(2)填空:已知∠P=40°,AB=12cm,点Q在 ![]() 上,从点A开始以πcm/s的速度逆时针运动到点C停止,设运动时间为ts. ①当t=时,以点A、Q、B、C为顶点的四边形面积最大;
上,从点A开始以πcm/s的速度逆时针运动到点C停止,设运动时间为ts. ①当t=时,以点A、Q、B、C为顶点的四边形面积最大;
②当t=时,四边形AQBC是矩形.
参考答案:
【答案】
(1)证明:如图1中,连接OC.

∵PC是切线,OC是半径,
∴OC⊥PC,
∴∠PCO=90°
∴∠PCA+∠ACO=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠B+∠CAB=90°,
∵OC=OA,
∴∠OAC=∠OCA,
∴∠B+∠OCA=90°,
∴∠PCA=∠B.
(2)3s;![]()
【解析】解:(2)①如图2中,当点Q在AB下方, ![]() =
= ![]() 时,四边形AQBC的面积最大,此时t=
时,四边形AQBC的面积最大,此时t= ![]() =3s.
=3s. 
所以答案是3s.
②如图3中,当 ![]() =
= ![]() 时,四边形AQBC是矩形,连接CQ与AB交于点O.
时,四边形AQBC是矩形,连接CQ与AB交于点O.
∵∠P=40°,∠PCO=90°,
∴∠POC=50°,
∴∠AOQ=130°,
∴弧AQ的长= ![]() =
= ![]() ,
,
∴t= ![]() =
= ![]() s.
s.
所以答案是 ![]() s.
s.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=8,动点P从点A出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
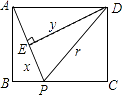
A.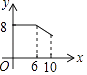
B.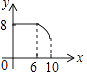
C.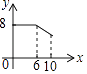
D.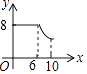
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(1,
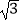 )在反比例函数y=
)在反比例函数y= 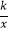 (x>0)的图象上,连接OA,将线段OA绕点O沿顺时针方向旋转30°,得到线段OB.
(x>0)的图象上,连接OA,将线段OA绕点O沿顺时针方向旋转30°,得到线段OB.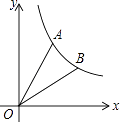
(1)求反比例函数的解析式;
(2)填空:
①点B的坐标是;
②判断点B是否在反比例函数的图象上?答;
③设直线AB的解析式为y=ax+b,则不等式ax+b﹣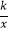 <0的解集是 .
<0的解集是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=ax2+bx+c(a≠0)中的x和y满足下表:
x
…
0
1
2
3
4
5
…
y
…
3
0
﹣1
0
m
8
…
(1)可求得m的值为;
(2)求出这个二次函数的解析式;
(3)当y>3时,x的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,矩形ABCD中,AB=2,BC=5,BP=1,∠MPN=90°,将∠MPN绕点P从PB处开始按顺时针方向旋转,PM交边AB(或AD)于点E,PN交边AD(或CD)于点F,当PN旋转至PC处时,∠MPN的旋转随即停止.
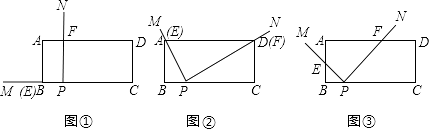
(1)特殊情形:如图②,发现当PM过点A时,PN也恰巧过点D,此时,△ABP△PCD(填“≌”或“~”);
(2)类比探究:如图③,在旋转过程中,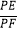 的值是否为定值?若是,请求出该定值;若不是,请说明理由.
的值是否为定值?若是,请求出该定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角△ABC中,边BC长为12,高AD长为8.
(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.
①求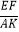 的值;
的值;
②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值;
(2)若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+bx+c过点A(4,0),B(﹣4,﹣4).
x2+bx+c过点A(4,0),B(﹣4,﹣4). 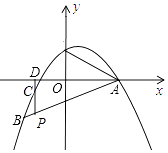
(1)求抛物线的解析式;
(2)若点P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交抛物线及x轴于C、D两点.请问是否存在这样的点P,使PD=2CD?若存在,请求出点P的坐标;若不存在,请说明理由.
相关试题

