【题目】如图,已知直线AC∥BD,且直线AB和AC、BD分别交于A、B两点,直线CD和AC、BD分别交于C、D两点,点P在直线AB上.
(1)如果点P在A、B两点之间运动时(如图1),试找出∠PCA、∠PDB、∠CPD之间的关系,并说出理由;
(2)如果点P在A、B两点外侧运动时(如图2,图3),问∠PCA、∠PDB、∠CPD之间的关系是否发生变化?试分别利用图2,图3探究∠PCA、∠PDB、∠CPD之间的关系(点P和A、B不重合).

参考答案:
【答案】∠CPD=∠PCA+∠PDB,理由见解析;(2)①当点P在线段AB的延长线上运动时,∠CPD=∠PCA-∠PDB;②当点P在线段BA的延长线上运动时,∠CPD=∠PDB-∠PCA.
【解析】
(1)过点P作a的平行线,根据平行线的性质进行求解;
(2)①当点P在线段AB的延长线上运动时,过点P作b的平行线PE,由平行线的性质可得出a∥b∥PE,由此即可得出结论;②当点P在线段BA的延长线上运动时,设直线AC与DP交于点F,由三角形外角的性质可得出∠1+∠3=∠PFA,再由平行线的性质即可得出结论.
(1)如图1,过点P作PE∥a,则∠1=∠CPE.
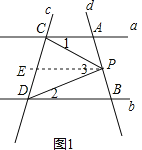
∵a∥b,PE∥a,
∴PE∥b,
∴∠2=∠DPE,
∴∠3=∠1+∠2,
即∠CPD=∠PCA+∠PDB;
(2)①当点P在线段AB的延长线上运动时,∠CPD=∠PCA-∠PDB.
理由:如图2,过点P作PE∥b,则∠2=∠EPD,
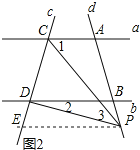
∵直线a∥b,
∴a∥PE,
∴∠1=∠EPC,
∵∠3=∠EPC-∠EPD,
∴∠3=∠1-∠2,
即∠CPD=∠PCA-∠PDB;
②当点P在线段BA的延长线上运动时,∠CPD=∠PDB-∠PCA.
证明:如图3,设直线AC与DP交于点F,
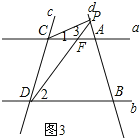
∵∠PFA是△PCF的外角,
∴∠PFA=∠1+∠3,
∵a∥b,
∴∠2=∠PFA,
∴∠2=∠1+∠3,
∴∠3=∠2-∠1,
即∠CPD=∠PDB-∠PCA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB=( )

A. 1∶
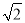 B. 1∶2 C.
B. 1∶2 C. 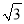 ∶2 D. 1∶
∶2 D. 1∶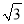
-
科目: 来源: 题型:
查看答案和解析>>【题目】将四张边长各不相同的正方形纸片按如图方式放入矩形
 内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示.设右上角与左下角阴影部分的周长的差为
内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示.设右上角与左下角阴影部分的周长的差为 .若知道
.若知道 的值,则不需测量就能知道周长的正方形的标号为( )
的值,则不需测量就能知道周长的正方形的标号为( )
A.①B.②C.③D.④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,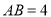 ,
, ,点
,点 在斜边
在斜边 上,连接
上,连接 ,把
,把 沿直线
沿直线 翻折,使点
翻折,使点 落在同一平面内的点
落在同一平面内的点 处.当
处.当 与
与 的直角边垂直时,
的直角边垂直时, 的长为__________.
的长为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 、
、 的垂直平分线
的垂直平分线 、
、 相交于点
相交于点 ,若
,若 等于
等于 ,则
,则 _____________
_____________ .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)若△ABC和△A1B1C1关于原点O成中心对称图形,画出△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2;
(3)在x轴上存在一点P,满足点P到点B1与点C1距离之和最小,请直接写出P B1+ P C1的最小值为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(m﹣1)x2﹣x﹣2=0.
(1)若x=﹣1是方程的一个根,求m的值和方程的另一根;
(2)当m为何实数时,方程有实数根;
(3)若x1,x2是方程的两个根,且
 ,试求实数m的值.
,试求实数m的值.
相关试题

