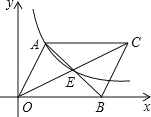
【题目】如图,平行四边形AOBC中,对角线交于点E,双曲线y=![]() (k>0)经过A、E两点, 若平行四边形AOBC的面积为30,则k=__________.
(k>0)经过A、E两点, 若平行四边形AOBC的面积为30,则k=__________.
参考答案:
【答案】10
【解析】如图,过A作AD⊥OB于D,EF⊥OB于F,设A(x,![]() ),B(a,0),得到EF为△ABD的中位线,可表示出EF的长,由OB-OD可得BD的长,根据F为BD的中点,得到FB的长,由OB-FB可得出OF的长,表示出E的坐标,代入反比例解析式中,得到a=3x,再由BO与AD的积为平行四边形的面积,表示出平行四边形的面积,根据平行四边形AOBC的面积为30,列出等式,将a=3x代入可得出k的值.
),B(a,0),得到EF为△ABD的中位线,可表示出EF的长,由OB-OD可得BD的长,根据F为BD的中点,得到FB的长,由OB-FB可得出OF的长,表示出E的坐标,代入反比例解析式中,得到a=3x,再由BO与AD的积为平行四边形的面积,表示出平行四边形的面积,根据平行四边形AOBC的面积为30,列出等式,将a=3x代入可得出k的值.
如图,过A作AD⊥OB于D,EF⊥OB于F,设A(x,![]() ),B(a,0),
),B(a,0),

∵四边形AOBC是平行四边形,
∴AE=EB,
∴EF为△ABD的中位线,
∴EF=![]() AD=
AD=![]() ,DF=
,DF=![]() (a-x),OF=OD+DF=
(a-x),OF=OD+DF=![]() ,
,
∴E(![]() ,
,![]() ),
),
∵E在双曲线y=![]() 上,
上,
∴![]()
![]() =k,
=k,
∴a=3x,
∵SAOBC=OBAD=30,
∴a![]() =3x
=3x![]() =3k=30,
=3k=30,
解得:k=10.
故答案为:10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的限距点的定义如下:若P′为直线PC与⊙C的一个交点,满足r≤PP′≤2r,则称P′为点P关于⊙C的限距点,如图为点P及其关于⊙C的限距点P′的示意图.

(1)当⊙O的半径为1时.
①分别判断点M(3,4),N( ,0),T(1,
,0),T(1,  )关于⊙O的限距点是否存在?若存在,求其坐标;
)关于⊙O的限距点是否存在?若存在,求其坐标;
②点D的坐标为(2,0),DE,DF分别切⊙O于点E,点F,点P在△DEF的边上.若点P关于⊙O的限距点P′存在,求点P′的横坐标的取值范围;
(2)保持(1)中D,E,F三点不变,点P在△DEF的边上沿E→F→D→E的方向运动,⊙C的圆心C的坐标为(1,0),半径为r,请从下面两个问题中任选一个作答.问题1
问题2
若点P关于⊙C的限距点P′存在,且P′随点P的运动所形成的路径长为πr,则r的最小值为
.若点P关于⊙C的限距点P′不存在,则r的取值范围为
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边△ABC的边长为4cm,点P,Q分别从B,C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;
点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s),
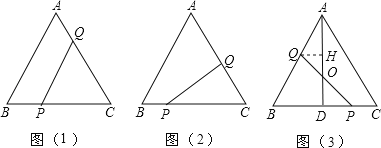
(1)如图(1),当x为何值时,PQ∥AB;
(2)如图(2),若PQ⊥AC,求x;
(3)如图(3),当点Q在AB上运动时,PQ与△ABC的高AD交于点O,OQ与OP是否总是相等?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知动点P在函数
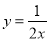 (x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AFBE的值为( )
(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AFBE的值为( )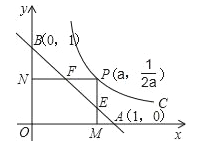
A. 4 B. 2 C. 1 D.
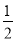
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x的二次函数,当x=2时,y=﹣4,当y=4时,x恰为方程2x2﹣x﹣8=0的根.
(1)解方程 2x2﹣x﹣8=0
(2)求这个二次函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE∥BC,DE=EF,AE=EC,则图中的四边形ADCF是__,四边形BCFD是__.(选填“平行四边形、矩形、菱形、正方形”)

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣0.125×18
 ×8
×8(2)﹣24×(
 ﹣
﹣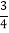 +
+ )
)(3)91
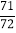 ×(﹣36)
×(﹣36)(4)﹣4×(﹣8
 )+(﹣8)×(﹣8
)+(﹣8)×(﹣8 )+12×(﹣8
)+12×(﹣8 )
)
相关试题

