【题目】如图,△ABC中,∠A=∠ABC,DE垂直平分BC,交BC于点D,交AC于点E.

(1)若AB=5,BC=8,求△ABE的周长;
(2)若BE=BA,求∠C的度数.
参考答案:
【答案】(1)13(2)36°
【解析】
(1)由等边对等角可知AC=BC=8,由线段垂直平分线的性质可知CE=BE,进而可求△ABE的周长;
(2)由BE=CE可知∠C=∠CBE,由外角性质可得∠BEA=2∠C,由BE=BA可证∠A=∠BEA=2∠C,然后利用三角形内角和等于180°列式求解即可.
(1)解:∵△ABC中,∠A=∠ABC
∴AC=BC=8
∵DE垂直平分BC,
EB=EC
又∵AB=5,
∴△ABE的周长为:
AB+AE+EB=AB+(AE+EC)=AB+AC=5+8=13
(2)解:∵EB=EC
∴∠C=∠CBE
∵∠AEB=∠C+∠CBE
∴∠BEA=2∠C
∵BE=BA
∴∠AEB=∠A
又∵AC=BC
∴∠CBA=∠A=2∠C
∵∠CBA+∠A+∠C=180°
∴5∠C=180°
∴∠C=36°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=﹣
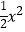 +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).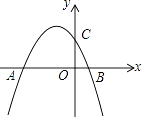
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
(1)已知:如图,∠AOC=∠BOC,点P在OC上,________
求证:________.
请你补全已知和求证
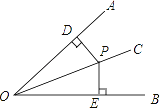
(2)并写出证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于圆O,∠BAD=90°,AC为直径,过点A作圆O的切线交CB的延长线于点E,过AC的三等分点F(靠近点C)作CE的平行线交AB于点G,连结CG.

(1)求证:AB=CD;
(2)求证:CD2=BEBC;
(3)当CG=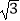 ,BE=
,BE=  时,求CD的长.
时,求CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(时)之间的关系的图象如图所示.根据图中提供的信息,有下列说法:①他们都行驶了18千米;②甲在中途停留了0.5小时;③乙比甲晚出发了0.5小时;④甲、乙两人同时到达目的地;⑤乙追上甲后甲的速度<乙的速度.其中符合图象描述的说法有( )
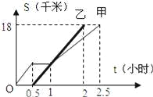
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】把所有正奇数从小到大排列,并按如下规律分组:(1)(3,5,7)、(9,11,13,15,17),(19,21,23,25,27,29,31),…,现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A89=( )
A.(6,7)
B.(7,8)
C.(7,9)
D.(6,9) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB:y=0.5x+1分别与x轴、y轴交于点A,点B,直线CD:y=x+b分别与x轴,y轴交于点C,点D.直线AB与CD相交于点P,已知S△ABD=4,则点P的坐标是( )
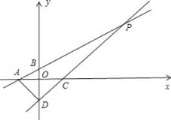
A. (3,2.5) B. (8,5) C. (4,3) D. (0.5,1.25)
相关试题

