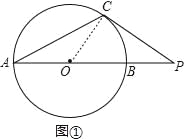
【题目】在⊙O中,AB为直径,C为⊙O上一点.

(1)如图1,过点C作⊙O的切线,与AB延长线相交于点P,若∠CAB=27°,求∠P的度数;
(2)如图2,D为弧AB上一点,OD⊥AC,垂足为E,连接DC并延长,与AB的延长线交于点P,若∠CAB=10°,求∠P的大小.
参考答案:
【答案】(1)∠P =36°;(2)∠P=30°.
【解析】
试题(Ⅰ)连接OC,首先根据切线的性质得到∠OCP=90°,利用∠CAB=27°得到∠COB=2∠CAB=54°,然后利用直角三角形两锐角互余即可求得答案;
(Ⅱ)根据E为AC的中点得到OD⊥AC,从而求得∠AOE=90°﹣∠EAO=80°,然后利用圆周角定理求得∠ACD=![]() ∠AOD=40°,最后利用三角形的外角的性质求解即可.
∠AOD=40°,最后利用三角形的外角的性质求解即可.
试题解析:(Ⅰ)如图,连接OC,
∵⊙O与PC相切于点C,
∴OC⊥PC,即∠OCP=90°,
∵∠CAB=27°,
∴∠COB=2∠CAB=54°,
在Rt△AOE中,∠P+∠COP=90°,
∴∠P=90°﹣∠COP=36°;
(Ⅱ)∵E为AC的中点,
∴OD⊥AC,即∠AEO=90°,
在Rt△AOE中,由∠EAO=10°,
得∠AOE=90°﹣∠EAO=80°,
∴∠ACD=![]() ∠AOD=40°,
∠AOD=40°,
∵∠ACD是△ACP的一个外角,
∴∠P=∠ACD﹣∠A=40°﹣10°=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店将进货价每个10元的商品按售价18元售出时,每天可卖出60个.商店经理到市场上做了一番调查后发现,若将这种商品的售价每提高1元,则日销售量就减少5个;若将这种商品的售价每降低1元,则日销售量就增加10个。为获得每日最大利润,此商品售价应定为每个多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
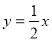 与双曲线
与双曲线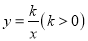 交于
交于 、
、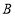 两点,且点
两点,且点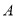 的横坐标为4.
的横坐标为4.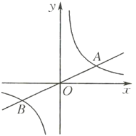
(1)若双曲线
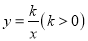 上一点
上一点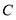 的纵坐标为8,求
的纵坐标为8,求 的面积;
的面积;(2)过原点
 的另一条直线
的另一条直线 交双曲线
交双曲线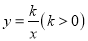 于
于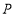 ,
,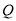 两点(点
两点(点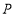 在第一象限),若由点
在第一象限),若由点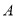 ,
,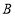 ,
,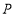 ,
,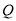 为顶点组成的四边形面积为24,求点
为顶点组成的四边形面积为24,求点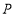 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC内接于⊙O,过点A作直线EF.
(1)如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).
(ī) (īī) (īīī)
(2)如图(2),若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且
 ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.(1)求证:CD是⊙O的切线;
(2)若CD=2
 ,求⊙O的半径.
,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=540,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F。

(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求
 的长。
的长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,
 中,
中, ,点
,点 是边
是边 上一点,过点
上一点,过点 作
作 交
交 于点
于点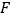
 如图①,求证:
如图①,求证: ;
;  如图②,将
如图②,将 绕点
绕点 逆时针旋转
逆时针旋转 得到
得到 .连接
.连接 .
.①若
 ,求
,求 的长;
的长;②若
 ,在图②的旋转过程中,当
,在图②的旋转过程中,当 时,直接写出旋转角
时,直接写出旋转角 的大小.
的大小. 
相关试题

