Question

【题目】如图，在△ABC中，AB=AC，∠BAC=540，以AB为直径的⊙O分别交AC，BC于点D，E，过点B作⊙O的切线，交AC的延长线于点F。

（1）求证：BE=CE；

（2）求∠CBF的度数；

（3）若AB=6，求的长。

Answer 1

【答案】解：（1）如图，连接AE，

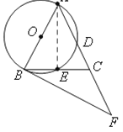
∵AB是⊙O的直径，

∴∠AEB＝900，即AE⊥BC。

又∵AB=AC，∴BE=CE。

（2）∵∠BAC=540，AB=AC，∴∠ABC=630。

又∵BF是⊙O的切线，∴∠ABF＝900。

∴∠CBF＝∠ABF一∠ABC＝270。

（3）连接OD，

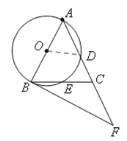
∵OA=OD，∠BAC=540，∴∠AOD＝720。

又∵AB=6，∴OA=2。

∴。

【解析】（1）连接AE，则根据直径所对圆周角是直角的性质得AE⊥BC，从而根据等腰三角形三线合一的性质得出结论。

（2）由∠BAC=540，AB=AC，根据等腰三角形等边对等角的性质和三角形内角和等于零180度求得∠ABC=630；由切线垂直于过切点直径的性质得∠ABF＝900，从而由∠CBF＝∠ABF一∠ABC得出结论。

（3）连接OD，根据同弧所对圆周角是圆心角一半的性质，求得∠AOD＝720，根据弧长公式即可求。