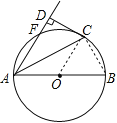
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

参考答案:
【答案】 (2)4
【解析】
试题(1)连结OC,由![]() =
=![]() ,根据圆周角定理得∠FAC=∠BAC,而∠OAC=∠OCA,则∠FAC=∠OCA,可判断OC∥AF,由于CD⊥AF,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
,根据圆周角定理得∠FAC=∠BAC,而∠OAC=∠OCA,则∠FAC=∠OCA,可判断OC∥AF,由于CD⊥AF,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
(2)连结BC,由AB为直径得∠ACB=90°,由![]() =
=![]() =
=![]() ,得∠BOC=60°,则∠BAC=30°,所以
,得∠BOC=60°,则∠BAC=30°,所以
∠DAC=30°,在Rt△ADC中,利用含30°的直角三角形三边的关系得AC=2CD=4![]() ,在Rt△ACB中,利用含30°的直角三角形三边的关系得BC=
,在Rt△ACB中,利用含30°的直角三角形三边的关系得BC=![]() AC=4,AB=2BC=8,所以⊙O的半径为4.
AC=4,AB=2BC=8,所以⊙O的半径为4.
试题解析:(1)证明:连结OC,如图,
∵![]() =
=![]()
∴∠FAC=∠BAC
∵OA=OC
∴∠OAC=∠OCA
∴∠FAC=∠OCA
∴OC∥AF
∵CD⊥AF
∴OC⊥CD
∴CD是⊙O的切线
(2)解:连结BC,如图
∵AB为直径
∴∠ACB=90°
∵![]() =
=![]() =
=![]()
∴∠BOC=![]() ×180°=60°
×180°=60°
∴∠BAC=30°
∴∠DAC=30°
在Rt△ADC中,CD=2![]()
∴AC=2CD=4![]()
在Rt△ACB中,BC=![]() AC=
AC=![]() ×4
×4![]() =4
=4
∴AB=2BC=8
∴⊙O的半径为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
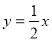 与双曲线
与双曲线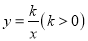 交于
交于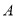 、
、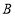 两点,且点
两点,且点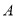 的横坐标为4.
的横坐标为4.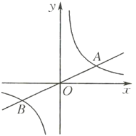
(1)若双曲线
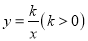 上一点
上一点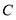 的纵坐标为8,求
的纵坐标为8,求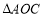 的面积;
的面积;(2)过原点
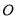 的另一条直线
的另一条直线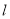 交双曲线
交双曲线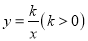 于
于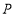 ,
,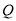 两点(点
两点(点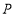 在第一象限),若由点
在第一象限),若由点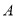 ,
,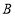 ,
,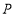 ,
,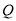 为顶点组成的四边形面积为24,求点
为顶点组成的四边形面积为24,求点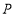 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC内接于⊙O,过点A作直线EF.
(1)如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).
(ī) (īī) (īīī)
(2)如图(2),若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在⊙O中,AB为直径,C为⊙O上一点.

(1)如图1,过点C作⊙O的切线,与AB延长线相交于点P,若∠CAB=27°,求∠P的度数;
(2)如图2,D为弧AB上一点,OD⊥AC,垂足为E,连接DC并延长,与AB的延长线交于点P,若∠CAB=10°,求∠P的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=540,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F。

(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求
 的长。
的长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,
 中,
中, ,点
,点 是边
是边 上一点,过点
上一点,过点 作
作 交
交 于点
于点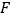
 如图①,求证:
如图①,求证: ;
;  如图②,将
如图②,将 绕点
绕点 逆时针旋转
逆时针旋转 得到
得到 .连接
.连接 .
.①若
 ,求
,求 的长;
的长;②若
 ,在图②的旋转过程中,当
,在图②的旋转过程中,当 时,直接写出旋转角
时,直接写出旋转角 的大小.
的大小. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为( )

A. 30 B. 50 C. 66 D. 80
相关试题

