【题目】数学老师布置了一道思考题,“计算:(﹣![]() )÷(
)÷(![]() ﹣
﹣![]() )”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
)”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
小明的解法:原式的倒数为(![]() ﹣
﹣![]() )÷(﹣
)÷(﹣![]() )…第一步
)…第一步
=(![]() ﹣
﹣![]() )×(﹣12)…第二步
)×(﹣12)…第二步
=﹣4+10…第三步
=6…第四步
所以(﹣![]() )÷(
)÷(![]() ﹣
﹣![]() )=
)=![]() .
.
(1)小明解法第二步到第三步的运算依据是什么?
(2)请你运用小明的解法计算:(﹣![]() )÷(
)÷(![]() ﹣
﹣![]() +
+![]() ).
).
参考答案:
【答案】(1)第二步到第三步的运算依据是乘法分配律;(2)![]() .
.
【解析】
(1)根据题目中的解答过程可以看出第二步到第三步的依据,本题得以解决;
(2)根据题目中的例子可以解答本题.
解:(1)由题意可得,
小明解法第二步到第三步的运算依据是乘法分配律;
(2)![]()
![]()
=(﹣8)+4+(﹣9)
=﹣13,
∴(﹣![]() )÷(
)÷(![]() ﹣
﹣![]() +
+![]() )=
)=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=
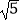 ,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为 .
,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为 . 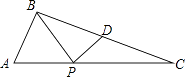
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明随机调查了若干市民租用公共自行车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如图统计图,请根据图中信息,解答下列问题:

(1)这次被调查的总人数是多少?
(2)试求表示A组的扇形圆心角的度数,并补全条形统计图.
(3)如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)﹣2﹣1+(﹣16)﹣(﹣13);
(2)25÷5×(﹣
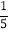 )÷(﹣
)÷(﹣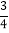 );
);(3)99
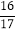 ×(﹣17);
×(﹣17);(4)﹣42+1
 ÷|﹣
÷|﹣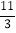 |×(
|×( ﹣2)2
﹣2)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC.
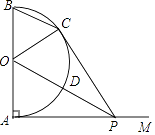
(1)求证:△OAP≌△OCP;
(2)若半圆O的半径等于2,填空: ①当AP=时,四边形OAPC是正方形;
②当AP=时,四边形BODC是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】数学小组的两位同学准备测量两幢教学楼之间的距离,如图,两幢教学楼AB和CD之间有一景观池(AB⊥BD,CD⊥BD),一同学在A点测得池中喷泉处E点的俯角为42°,另一同学在C点测得E点的俯角为45°(点B,E,D在同一直线上),两个同学已经在学校资料室查出楼高AB=15m,CD=20m,求两幢教学楼之间的距离BD.
(结果精确到0.1m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)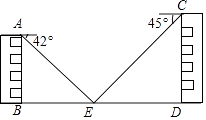
-
科目: 来源: 题型:
查看答案和解析>>【题目】一架长2.5m的梯子斜靠在竖直的墙上,这时梯足到墙的底端距离为0.7m,若梯子顶端下滑0.4m,则梯足将向外移
A、0.6mB、0.7m C、0.8mD、0.9m
相关试题

