【题目】如图,△ABC中,AB= ![]() ,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为 .
,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为 . 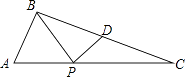
参考答案:
【答案】2或5﹣ ![]()
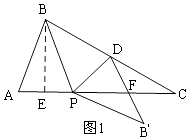
【解析】解:分两种情况:①当点B′在AC的下方时,如图1,
∵D是BC中点,
∴S△BPD=S△PDC,
∵S△PDF= ![]() S△BPD,
S△BPD,
∴S△PDF= ![]() S△PDC,
S△PDC,
∴F是PC的中点,
∴DF是△BPC的中位线,
∴DF∥BP,
∴∠BPD=∠PDF,
由折叠得:∠BPD=∠B′PD,
∴∠B′PD=∠PDF,
∴PB′=B′D,
即PB=BD,
过B作BE⊥AC于E,
Rt△ABE中,tan∠A= ![]() =2,
=2,
∵AB= ![]() ,
,
∴AE=1,BE=2,
∴EC=5﹣1=4,
由勾股定理得:BC= ![]() =
= ![]() =2
=2 ![]() ,
,
∵D为BC的中点,
∴BD= ![]() ,
,
∴PB=BD= ![]() ,
,
在Rt△BPE中,PE=1,
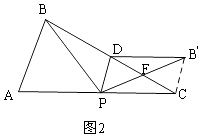
∴AP=AE+PE=1=1=2;②当点B'在AC的上方时,如图2,连接B′C,
同理得:F是DC的中点,F是PB′的中点,
∴DF=FC,PF=FB′,
∴四边形DPCB′是平行四边形,
∴PC=B′D=BD= ![]() ,
,
∴AP=5﹣ ![]() ,
,
综上所述,AP的长为2或5﹣ ![]() ;
;
所以答案是:2或5﹣ ![]() .
.
【考点精析】利用翻折变换(折叠问题)和解直角三角形对题目进行判断即可得到答案,需要熟知折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】把三张形状、大小均相同但画面不同的风景图片都按同样的方式剪成相同的两片,然后堆放到一起混合洗匀,背面朝上,从这堆图片中随机抽出两张,这两张图片恰好能组成一张原风景图片的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形正确的是( )
A. 4x﹣5=3x+2变形得 4x﹣3x=2﹣5
B.
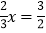 变形得x=1
变形得x=1C. 3(x﹣1)=2(x+3)变形得3x﹣1=2x+6
D.
 变形得3x=15
变形得3x=15 -
科目: 来源: 题型:
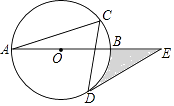
查看答案和解析>>【题目】如图,⊙O的半径是4,圆周角∠C=60°,点E时直径AB延长线上一点,且∠DEB=30°,则图中阴影部分的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明随机调查了若干市民租用公共自行车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如图统计图,请根据图中信息,解答下列问题:

(1)这次被调查的总人数是多少?
(2)试求表示A组的扇形圆心角的度数,并补全条形统计图.
(3)如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)﹣2﹣1+(﹣16)﹣(﹣13);
(2)25÷5×(﹣
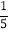 )÷(﹣
)÷(﹣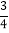 );
);(3)99
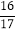 ×(﹣17);
×(﹣17);(4)﹣42+1
 ÷|﹣
÷|﹣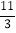 |×(
|×( ﹣2)2
﹣2)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】数学老师布置了一道思考题,“计算:(﹣
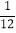 )÷(
)÷( ﹣
﹣ )”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
)”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.小明的解法:原式的倒数为(
 ﹣
﹣ )÷(﹣
)÷(﹣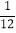 )…第一步
)…第一步=(
 ﹣
﹣ )×(﹣12)…第二步
)×(﹣12)…第二步=﹣4+10…第三步
=6…第四步
所以(﹣
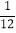 )÷(
)÷( ﹣
﹣ )=
)= .
.(1)小明解法第二步到第三步的运算依据是什么?
(2)请你运用小明的解法计算:(﹣
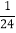 )÷(
)÷( ﹣
﹣ +
+ ).
).
相关试题

