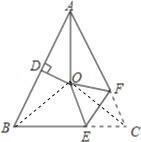
【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CEF的度数为______.

参考答案:
【答案】50°
【解析】
如图,作出辅助线,首先求出∠BAO=25°,根据线段垂直平分线的性质和等腰三角形的性质求出∠ABO=25°,进而求出∠OBC=40°,然后证明△ABO≌△ACO,得出OB=OC,得出∠OCB=40°,根据折叠的性质和等腰三角形的性质求出∠COE=∠OCB=40°问题即可解决.
解:连接OB、OC,
∵∠BAC=50°,AO为∠BAC的平分线,
∴∠BAO=![]() ∠BAC=25°.
∠BAC=25°.
又∵AB=AC,
∴∠ABC=∠ACB=![]() (180°-50°)=65°.
(180°-50°)=65°.
∵DO是AB的垂直平分线,
∴OA=OB,
∴∠ABO=∠BAO=25°.
∴∠OBC=∠ABC-∠ABO=65°-25°=40°.
在△ABO和△ACO中
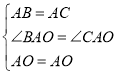 ,
,
∴△ABO≌△ACO(SAS),
∴OB=OC,
∴∠OCB=∠OBC=40°.
∵将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,
∴OE=CE,
∴∠COE=∠OCB=40°.
在△OCE中,
∠OEC=180°-∠COE-∠OCB=180°-40°-40°=100°,
由折叠的性质可得:∠CEF=∠OEF=50°.
故答案为:50°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,恒有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”,同理函数y=x也是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=
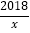 是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;(2)如果已知二次函数y=x2﹣4x+k是闭区间[2,t]上的“闭函数”,求k和t的值;
(3)如果(2)所述的二次函数的图象交y轴于C点,A为此二次函数图象的顶点,B为直线x=1上的一点,当△ABC为直角三角形时,写出点B的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,过B作⊙O的切线,在该切线上取点C,连接AC交⊙O于D,若⊙O的半径是6,∠C=36°,则劣弧AD的长是( )

A.
 B.
B.  C.
C.  D. 3π
D. 3π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图.在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点.若DE平分△ABC的周长,则DE的长是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中有两点A(0,1),B(﹣1,0),动点P在反比例函数y=
 的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

相关试题

