【题目】在△ABC中,∠B=40°,过点A的直线将这个三角形分成两个等腰三角形,则∠C的度数为______________.
参考答案:
【答案】20°或50°或80°
【解析】
先画出图形,再根据∠B为底角或顶角两种情况讨论;由△ABD形状的改变而引起△ACD的形状发生改变,可求出∠C的度数.
解:应分四种情况进行讨论:
当AD=AC,AD=BD时,如图①所示,
∠BAD=∠B=40°,∠C=∠ADC.
∵∠BAD+∠B+∠ADB=180°,
∴∠ADB=180°-2×40°=100°,
∴∠ADC=180°-∠ADB=80°,
∴∠C=80°;
当AC=DC,BD=AD时,如图①所示,
∠DAC=∠ADC=180°-∠ADB=∠B+∠BAD=80°,
∴∠C=180°-∠ADC-∠DAC=20°;
当AD=DC,AB=AD时,如图②所示,
∠C=∠DAC,∠ADB=∠B=40°.
∴∠ADC=180°-∠ADB=140°,
∴∠C=![]() (180°-∠ADC)=20°;
(180°-∠ADC)=20°;
当AD=BD,AD=CD时,如图①所示,
∠BAD=∠B=40°,∠ADC=180°-∠ADB=∠B+∠BAD=80°,
∠C=∠DAC=![]() (180°-∠ADC)=
(180°-∠ADC)=![]() ×(180°-80°)=50°.
×(180°-80°)=50°.
综上所述,∠C的度数为80°或20°或50°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把一副普通扑克牌中的4张;黑桃2,红心3,梅花4,黑桃5,洗匀后正面朝下放在桌面上.
(1)从中随机抽取一张牌是黑桃的概率是多少?
(2)从中随机抽取一张,再从剩下的牌中随机抽取另一张. 请用表格或树状图表示抽取的两张牌牌面数字所有可能出现的结果,并求抽取的两张牌牌面数字之和大于7的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同),其中红球有2个,黄球有1个,从中任意捧出1球是红球的概率为

(1)试求袋中绿球的个数;

(2)第1次从袋中任意摸出l球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形
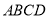 中,E为
中,E为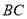 边上一点,连接
边上一点,连接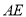 ,作
,作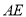 的垂直平分线交
的垂直平分线交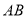 于G,交
于G,交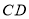 于F,若
于F,若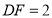 ,
, ,则
,则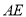 的长为( )
的长为( )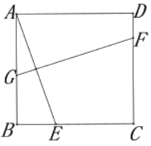
A.
 B.
B. C.10D.12
C.10D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小强为了测量一幢高楼的高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C的视线PC与地面夹角∠DPC=36°,测得楼顶A的视线PA与地面夹角∠APB=54°,测得P到楼底距离PB与旗杆高度都为10米,测得旗杆与楼之间的距离DB=36米,据此小强计算出了楼高,求楼高AB是多少米.
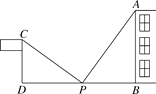
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点E在BC上,CD⊥AB,EF⊥AB,垂足分别为D、F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, ,
, ,
, 平分
平分 ,过点
,过点 作
作 于点
于点 ,延长
,延长 ,
, 交于点
交于点 ,下列结论中:①
,下列结论中:① ;②
;② ;③
;③ ;④
;④ .正确的是( )
.正确的是( )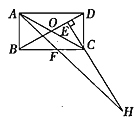
A.②③B.③④C.①②④D.②③④
相关试题

