【题目】如图1,在正方形ABCD中,P在对角线AC上,E在AC的延长线上,PB=PM , DE=EF.
(1)求证:∠CDE=∠F;
(2)若AB=5,CM=1,求PB的长;
(3)如图2,若BF=10,△QCF是以CF为底的等腰三角形,连接DQ , 试求△CDQ的最大面积.
参考答案:
【答案】
(1)
过E作EG⊥CF于G,EH⊥DC于H
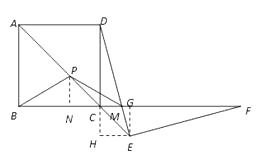
则四边形CHEG是矩形,
∵四边形ABCD是正方形,
∴∠ACB=∠ACD=45°,
∴∠ECG=∠ECH=45°,
∴CH=EH
∵矩形CHEG是正方形
∴EG=EH
又∵DE=EF,∴Rt△DEH≌Rt△FEG
∴∠CDE=∠F
(2)
解:过P作PN⊥BC于N
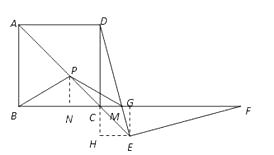
∵BC=AB=5,CM=1,∴BM=6
∵PB=PM,∴BN=NM=3,
∴NC=2
在Rt△PNC中,∵∠PCN=45°,
∴PN=NC=2
在Rt△PNM中,PM= ![]() =
= ![]() =
= ![]() ,
,
∴PB= ![]()
(3)
作QR⊥CF于R,QK⊥CD于K
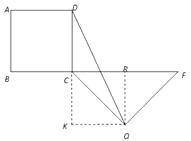
则四边形CKQR是矩形,
∴KQ=CR
又∵△QCF是以CF为底的等腰三角形,∴ CR=RF=![]() CF
CF
设BC=x,则CD=x,
KQ=CR=![]() CF=
CF=![]() (10-x)=5-
(10-x)=5-![]() x
x
∴S△CDQ=![]() CD·KQ=
CD·KQ=![]() ·x·(5-
·x·(5-![]() x)
x)
=-![]() x2+
x2+ ![]() x=-
x=-![]() (x-5)2+
(x-5)2+ ![]()
∴当x=5,△CDQ的面积有最大值 ![]()
【解析】
【考点精析】掌握等腰三角形的性质和勾股定理的概念是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点B按逆时针方向旋转得到△EBD,点E、点D分别与点A、点C对应,且点D在边AC上,边DE交边AB于点F,△BDC∽△ABC.已知BC=
 ,AC=5,那么△DBF的面积等于 .
,AC=5,那么△DBF的面积等于 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A、B两地相距4千米,上午11:00,甲从A地出发步行到B地,11:20乙从B地出发骑自行车到A地,甲乙两人离A地的距离(千米)与甲所用时间(分)之间的关系如图所示,由图中的信息可知,乙到达A地的时间为( )
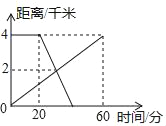
A. 上午11:40 B. 上午11:35 C. 上午11:45 D. 上午11:50
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(
 )﹣3+(﹣1)2017+
)﹣3+(﹣1)2017+ 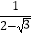 ﹣3sin60°.
﹣3sin60°. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知正比例函数的图象与反比例函数y=
 的图象交于点A(m,4).
的图象交于点A(m,4).
(1)求正比例函数的解析式;
(2)将正比例函数的图象向下平移6个单位得到直线l,设直线l与x轴的交点为B,求∠ABO的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】上海首条中运量公交线路71路已正式开通.该线路西起沪青平公路申昆路,东至延安东路中山东一路,全长17.5千米.71路车行驶于专设的公交车道,又配以专用的公交信号灯.经测试,早晚高峰时段71路车在专用车道内行驶的平均速度比在非专用车道每小时快6千米,因此单程可节省时间22.5分钟.求早晚高峰时段71路车在专用车道内行驶的平均车速.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,已知点R(1,0),点K(4,4),直线y=-
 x+b过点K , 分别交x轴、y轴于U、V两点,以点R为圆心, RK为半径作⊙R , ⊙R交x轴于A.
x+b过点K , 分别交x轴、y轴于U、V两点,以点R为圆心, RK为半径作⊙R , ⊙R交x轴于A.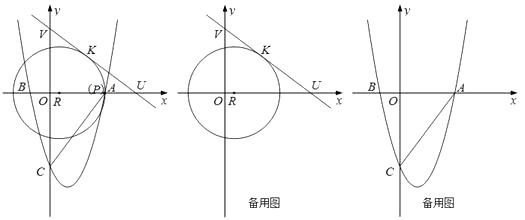
(1)若二次函数的图象经过点A、B(-2,0)、C(0,-8),求二次函数的解析式;
(2)判断直线UV与⊙R的位置关系,并说明理由;
(3)若动点P、Q同时从A点都以相同的速度分别沿AB、AC边运动,当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E , 使得以A、E、Q为顶点的三角形是等腰三角形.若存在,请求出E点坐标,若不存在,请说明理由.
相关试题

