【题目】如图所示,在平面直角坐标系中,已知点R(1,0),点K(4,4),直线y=- ![]() x+b过点K , 分别交x轴、y轴于U、V两点,以点R为圆心, RK为半径作⊙R , ⊙R交x轴于A.
x+b过点K , 分别交x轴、y轴于U、V两点,以点R为圆心, RK为半径作⊙R , ⊙R交x轴于A.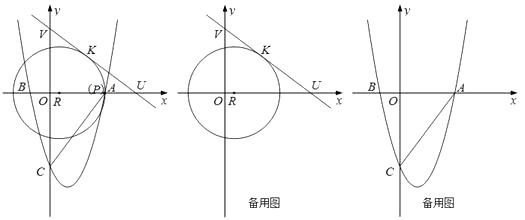
(1)若二次函数的图象经过点A、B(-2,0)、C(0,-8),求二次函数的解析式;
(2)判断直线UV与⊙R的位置关系,并说明理由;
(3)若动点P、Q同时从A点都以相同的速度分别沿AB、AC边运动,当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E , 使得以A、E、Q为顶点的三角形是等腰三角形.若存在,请求出E点坐标,若不存在,请说明理由.
参考答案:
【答案】
(1)
由K(4,4),R(1,0),
则RK=![]() ,
,
则OA=6,∴A(6,0),
设抛物线的解析式为y=a(x+2)(x-6),
把C(0,-8)代入得-8=a(0+2)(0-6),
解得a= ![]()
∴y= ![]() (x+2)(x-6)=
(x+2)(x-6)= ![]() x2-
x2- ![]() x-8
x-8
(2)
直线UV与⊙R相切
理由如下:
∵点K(4,4),直线y=-![]() x+b过点K,∴b=7
x+b过点K,∴b=7
对于y=-![]() x+7,当x=0时,y=7;当y=0时,x=
x+7,当x=0时,y=7;当y=0时,x=![]()
∴U(![]() ,0),V(0,7),∴OU=
,0),V(0,7),∴OU=![]() ,OV=7
,OV=7
连接RK,过K作KH⊥x轴于H
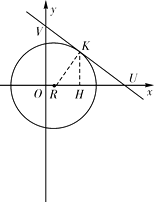
则RH=3,UH=![]() -4=
-4=![]() ,KH=4
,KH=4
∴ ![]() =
= ![]() =
=![]() ,
,
又∠RHK=∠KHU=90°,∴△RKH∽△KUH
∴∠KRH=∠UKH
∵∠RKH+∠KRH=90°,∴∠RKH+∠UKH=90°
即RK⊥UV
∴直线UV与⊙R相切
(3)
存在
分三种情况讨论:
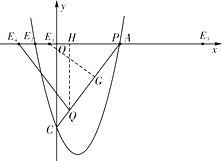
①若EQ=EA,作EG⊥AQ于G
则AG=GQ=![]() AQ=
AQ=![]() AB=4
AB=4
∵∠EAG=∠CAO,∠AGE=∠AOC=90°
∴△EAG∽△CAO,∴![]() =
=![]()
∵OA=6,OC=8,∴AC=10
∴ ![]() =
= ![]() ,∴AE=
,∴AE= ![]() ,∴OE=
,∴OE= ![]() -6=
-6= ![]()
∴E1(- ![]() ,0),
,0),
②若AE=AQ=8,则E2(-2,0),E3(14,0)
③QE=QA,作QH⊥x轴于H,则QH∥y轴
∴![]() =
=![]() ,∴
,∴ ![]() =
=![]()
∴AH= ![]() ,∴EH=AH=
,∴EH=AH= ![]() ,OH=6-
,OH=6- ![]() =
= ![]() ,∴EO=
,∴EO= ![]() -
- ![]() =
= ![]()
∴E4(- ![]() ,0)
,0)
综上,满足条件的E点有四个,E1(- ![]() ,0),E2(-2,0),E3(14,0),E4(-
,0),E2(-2,0),E3(14,0),E4(- ![]() ,0)
,0)
【解析】(1)要求抛物线解析式,先要求出点A的坐标,由OA=OR+RA,而RA是⊙R的半径,由R(1,0),K(4,4)可求出半径的长,从而可求得OA,即A的坐标,由A,B,是抛物线与x轴的交点,则可设两点式y=a(x+2)(x-6),再代入C的坐标,即可求出a的值;
(2)连接RK,则需证RK⊥UV , 可先根据点K(4,4),直线y=-![]() x+b过点K , 求出点b值,再求出U,V的坐标;不能直接运用勾股定理证明△RKU是直角三角形,则可过K作KH⊥x轴于H , 证明
x+b过点K , 求出点b值,再求出U,V的坐标;不能直接运用勾股定理证明△RKU是直角三角形,则可过K作KH⊥x轴于H , 证明 ![]() =
= ![]() =
=![]() , 又∠RHK=∠KHU=90°,则△RKH∽△KUH , 根据角的直角三角形的两个锐角和为90度,即可转换得到∠RKH+∠UKH=90°;
, 又∠RHK=∠KHU=90°,则△RKH∽△KUH , 根据角的直角三角形的两个锐角和为90度,即可转换得到∠RKH+∠UKH=90°;
(3)此题需作分类讨论:①若EQ=EA , 作EG⊥AQ于G , 通过证明△EAG∽△CAO , 由相应边成比例![]() =
=![]() 代入相应数据即可解出AE,则可得E的坐标;②若AE=AQ=8,由A的坐标直接可写出E的坐标;③若QE=QA , 根据相似构造平行线作QH⊥x轴于H , 则QH∥y轴,则由平行线分线段成比例可得
代入相应数据即可解出AE,则可得E的坐标;②若AE=AQ=8,由A的坐标直接可写出E的坐标;③若QE=QA , 根据相似构造平行线作QH⊥x轴于H , 则QH∥y轴,则由平行线分线段成比例可得![]() =
=![]() ,代入相应数据求出AH,则可求出点E的坐标.
,代入相应数据求出AH,则可求出点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,P在对角线AC上,E在AC的延长线上,PB=PM , DE=EF.

(1)求证:∠CDE=∠F;
(2)若AB=5,CM=1,求PB的长;
(3)如图2,若BF=10,△QCF是以CF为底的等腰三角形,连接DQ , 试求△CDQ的最大面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知正比例函数的图象与反比例函数y=
 的图象交于点A(m,4).
的图象交于点A(m,4).
(1)求正比例函数的解析式;
(2)将正比例函数的图象向下平移6个单位得到直线l,设直线l与x轴的交点为B,求∠ABO的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】上海首条中运量公交线路71路已正式开通.该线路西起沪青平公路申昆路,东至延安东路中山东一路,全长17.5千米.71路车行驶于专设的公交车道,又配以专用的公交信号灯.经测试,早晚高峰时段71路车在专用车道内行驶的平均速度比在非专用车道每小时快6千米,因此单程可节省时间22.5分钟.求早晚高峰时段71路车在专用车道内行驶的平均车速.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,AC为对角线,E是边AD上一点,BE⊥AC交AC于点F,BE、CD的延长线交于点G,且∠ABE=∠CAD.

(1)求证:四边形ABCD是矩形;
(2)如果AE=EG,求证:AC2=BCBG. -
科目: 来源: 题型:
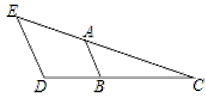
查看答案和解析>>【题目】如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,二次函数y=x2﹣2x+m(m>0)的对称轴与比例系数为5的反比例函数图象交于点A,与x轴交于点B,抛物线的图象与y轴交于点C,且OC=3OB.
(1)求点A的坐标;
(2)求直线AC的表达式;
(3)点E是直线AC上一动点,点F在x轴上方的平面内,且使以A、B、E、F为顶点的四边形是菱形,直接写出点F的坐标.
相关试题

