【题目】上海首条中运量公交线路71路已正式开通.该线路西起沪青平公路申昆路,东至延安东路中山东一路,全长17.5千米.71路车行驶于专设的公交车道,又配以专用的公交信号灯.经测试,早晚高峰时段71路车在专用车道内行驶的平均速度比在非专用车道每小时快6千米,因此单程可节省时间22.5分钟.求早晚高峰时段71路车在专用车道内行驶的平均车速.
参考答案:
【答案】解:设早晚高峰时段71路在专用车道内行驶的平均车速x千米/时. 根据题意,可列方程 ![]() ﹣
﹣ ![]() =
= ![]() .
.
整理得 x2﹣6x﹣280=0.
解得 x1=20,x2=﹣14.
经检验x1=20,x2=﹣14都是原方程的解.
因为速度不能负数,所以取x=20.
答:71路在专用车道内行驶的平均车速20千米/时.
【解析】设早晚高峰时段71路在专用车道内行驶的平均车速x千米/时.则非专用车道内行驶的平均速度是(x﹣6)千米/时,根据“单程可节省时间22.5分钟”列出方程并解答.
【考点精析】本题主要考查了分式方程的应用的相关知识点,需要掌握列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(
 )﹣3+(﹣1)2017+
)﹣3+(﹣1)2017+ 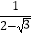 ﹣3sin60°.
﹣3sin60°. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,P在对角线AC上,E在AC的延长线上,PB=PM , DE=EF.

(1)求证:∠CDE=∠F;
(2)若AB=5,CM=1,求PB的长;
(3)如图2,若BF=10,△QCF是以CF为底的等腰三角形,连接DQ , 试求△CDQ的最大面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知正比例函数的图象与反比例函数y=
 的图象交于点A(m,4).
的图象交于点A(m,4).
(1)求正比例函数的解析式;
(2)将正比例函数的图象向下平移6个单位得到直线l,设直线l与x轴的交点为B,求∠ABO的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,已知点R(1,0),点K(4,4),直线y=-
 x+b过点K , 分别交x轴、y轴于U、V两点,以点R为圆心, RK为半径作⊙R , ⊙R交x轴于A.
x+b过点K , 分别交x轴、y轴于U、V两点,以点R为圆心, RK为半径作⊙R , ⊙R交x轴于A.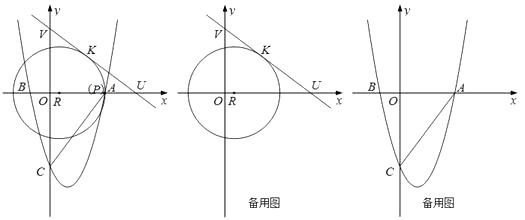
(1)若二次函数的图象经过点A、B(-2,0)、C(0,-8),求二次函数的解析式;
(2)判断直线UV与⊙R的位置关系,并说明理由;
(3)若动点P、Q同时从A点都以相同的速度分别沿AB、AC边运动,当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E , 使得以A、E、Q为顶点的三角形是等腰三角形.若存在,请求出E点坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,AC为对角线,E是边AD上一点,BE⊥AC交AC于点F,BE、CD的延长线交于点G,且∠ABE=∠CAD.

(1)求证:四边形ABCD是矩形;
(2)如果AE=EG,求证:AC2=BCBG. -
科目: 来源: 题型:
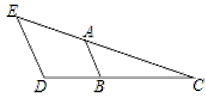
查看答案和解析>>【题目】如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)
相关试题

