【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法中正确的序号是_____.
①△ABE的面积等于△BCE的面积;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.

参考答案:
【答案】①②③
【解析】
根据等底等高的三角形的面积相等即可判断①;根据三角形内角和定理求出∠ABC=∠CAD,根据三角形的外角性质即可推出②;根据三角形内角和定理求出∠FAG=∠ACD,根据角平分线定义即可判断③;根据等腰三角形的判定判断④即可.
解:∵BE是中线,
∴AE=CE,
∴△ABE的面积=△BCE的面积(等底等高的三角形的面积相等),故①正确;
∵CF是角平分线,
∴∠ACF=∠BCF,
∵AD为高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ACB+∠CAD=90°,
∴∠ABC=∠CAD,
∵∠AFG=∠ABC+∠BCF,∠AGF=∠CAD+∠ACF,
∴∠AFG=∠AGF,故②正确;
∵AD为高,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,∠ABC+∠BAD=90°,
∴∠ACB=∠BAD,
∵CF是∠ACB的平分线,
∴∠ACB=2∠ACF,
∴∠BAD=2∠ACF,
即∠FAG=2∠ACF,故③正确;
根据已知条件不能推出∠HBC=∠HCB,即不能推出BH=CH,故④错误;
故答案为:①②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.

(1)作△ABC关于原点O成中心对称的△A1B1C1 .
(2)请写出点B关于y轴对称的点B2的坐标 . 若将点B2向下平移h单位,使其落在△A1B1C1内部(不包括边界),直接写出h的值(写出满足的一个即可). -
科目: 来源: 题型:
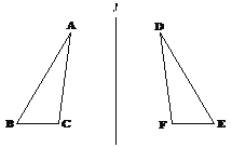
查看答案和解析>>【题目】如图所示,是用笔尖扎重叠的纸得到的成轴对称的图案,请根据图形写出:
(1)两组对应点:__________和__________;
(2)两组对应线段:__________和__________;
(3)两组对应角:__________和__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,过点B作BD⊥AC于点D,过D作DE∥BC,且DE=CD,连接CE,
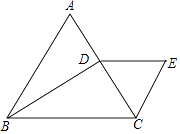
(1)求证:△CDE为等边三角形;
(2)请连接BE,若AB=4,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的
 后得到线段CD,则点B的对应点D的坐标为( )
后得到线段CD,则点B的对应点D的坐标为( ) 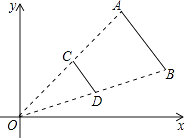
A.(3,3)
B.(1,4)
C.(3,1)
D.(4,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点M、N是∠ABC与∠ACB三等分线的交点,若∠A=60°,则∠BMN的度数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AD是∠BAC的平分线,交BC于点M,交⊙O于点D.则图中相似三角形共有( )

A.2对
B.4对
C.6对
D.8对
相关试题

