【题目】已知:如图,菱形ABCD中,AB=10cm,BD=12cm,对角线AC与BD相交于点O,直线MN以1cm/s从点D出发,沿DB方向匀速运动,运动过程中始终保持MN⊥BD,垂足是点P,过点P作PQ⊥BC,交BC于点Q.(0<t<6) 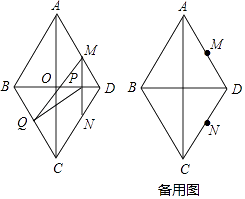
(1)求线段PQ的长;(用含t的代数式表示)
(2)设△MQP的面积为y(单位:cm2),求y与t的函数关系式;
(3)是否存在某时刻t,使线段MQ恰好经过点O?若存在求出此时t的值;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:如图1中,
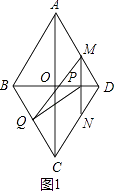
∵四边形ABCD是菱形,
∴BC=AB=10,OB=OD=6,BD⊥AC,
在Rt△BOC中,OC= ![]() =
= ![]() =8,
=8,
∴sin∠OBC= ![]() =
= ![]() ,
,
在Rt△PBQ中,∵PB=12﹣t,
sin∠PBQ= ![]() =
= ![]() ,
,
∴PQ= ![]() (12﹣t)=
(12﹣t)= ![]() ﹣
﹣ ![]() t(0<t<6)
t(0<t<6)
(2)
解:如图2中,作QH⊥MN于H.

∵∠QPH+∠BPQ=90°,∠BPQ+∠CBO=90°,
∴∠QPH=∠CBO,
∴QH=PQsin∠QPH= ![]() (
( ![]() ﹣
﹣ ![]() t),
t),
易知PM= ![]() t,
t,
∴y= ![]() PMQH=
PMQH= ![]()
![]() t
t ![]() (
( ![]() ﹣
﹣ ![]() t)=
t)= ![]() ﹣
﹣ ![]() t(0<t<6)
t(0<t<6)
(3)
解:如图3中,连接QN.
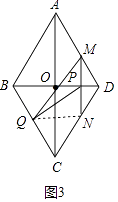
当MQ经过点O时,易证△BOQ≌△DOM,
∴BQ=DM,OM=OQ,
∵PM=PN,
∴OP∥QN,NQ=2OP,
∴QN⊥MN,QN= ![]() (
( ![]() ﹣
﹣ ![]() t),
t),
∴ ![]() (
( ![]() ﹣
﹣ ![]() t)=2(6﹣t),
t)=2(6﹣t),
解得t= ![]() ,
,
∴t= ![]() 时,MQ经过点O
时,MQ经过点O
【解析】【(1)如图1中,在Rt△BOC中,OC= ![]() =
= ![]() =8,推出sin∠OBC=
=8,推出sin∠OBC= ![]() =
= ![]() ,在Rt△PBQ中,由PB=12﹣t推出sin∠PBQ=
,在Rt△PBQ中,由PB=12﹣t推出sin∠PBQ= ![]() =
= ![]() ,即可求出PQ.(2)如图2中,作QH⊥MN于H.求出QH、PM即可解决问题.(3)如图3中,连接QN只要证明QM经过点O时,OP是△MQN的中位线,得到QN=2OP,由此列出方程即可解决问题.
,即可求出PQ.(2)如图2中,作QH⊥MN于H.求出QH、PM即可解决问题.(3)如图3中,连接QN只要证明QM经过点O时,OP是△MQN的中位线,得到QN=2OP,由此列出方程即可解决问题.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对相似三角形的应用的理解,了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).

(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围. -
科目: 来源: 题型:
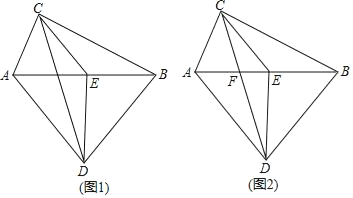
查看答案和解析>>【题目】如图,已知AC⊥BC,AD⊥BD,E为AB的中点,
(1)如图1,求证:△ECD是等腰三角形;
(2)如图2,CD与AB交点为F,若AD=BD,EF=3,DE=4,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列美丽的图案,是轴对称图形但不是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数
1
2
3
4
5
6
7
8
9
10
黑棋数
1
3
0
2
3
4
2
1
1
3
根据以上数据,估算袋中的白棋子数量为( )
A.60枚
B.50枚
C.40枚
D.30枚 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形ABCD沿直线EF折叠,若∠1=20°,则∠2=( )
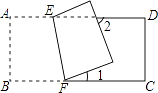
A.80°
B.70°
C.40°
D.20°
相关试题

