【题目】设x是实数,现在我们用{x}表示不小于x的最小整数,如{3.2}=4,{﹣2.6}=﹣2,{4}=4,{﹣5}=5.在此规定下任一实数都能写出如下形式:x={x}﹣b,其中0≤b<1.
(1)直接写出{x}与x,x+1的大小关系是 (由小到大);
(2)根据(1)中的关系式解决下列问题:
①求满足{3x+11}=6的x的取值范围;
②解方程:{3.5x+2}=2x﹣![]() .
.
参考答案:
【答案】(1)x≤{x}<x+1,(2)①﹣2<x≤﹣![]() ,②x=﹣
,②x=﹣![]() ,
,
【解析】
(1)x={x}﹣b,其中0≤b<1,b={x}﹣x,即0≤{x}﹣x<1,即可判断三者的大小关系,
(2)根据(1)中的关系得到关于x的一元一次不等式组,解之即可,
②根据(1)中的关系得到关于x的一元一次不等式组,且2x﹣![]() 为整数,即可求解.
为整数,即可求解.
(1)∵x={x}﹣b,其中0≤b<1,
∴b={x}﹣x,
即0≤{x}﹣x<1,
∴x≤{x}<x+1,
故答案为:x≤{x}<x+1,
(2)①∵{3x+11}=6,
∴3x+11≤6<(3x+11)+1,
解得:﹣2<x≤﹣![]() ,
,
即满足{3x+11}=6的x的取值范围为:﹣2<x≤﹣![]() ,
,
②∵{3.5x+2}=2x﹣![]() ,
,
∴3.5x+2≤2x﹣![]() <(3.5x+2)+1,且2x﹣
<(3.5x+2)+1,且2x﹣![]() 为整数,
为整数,
解不等式组得:﹣![]() <x≤﹣
<x≤﹣![]() ,
,
∴﹣![]() <2x﹣
<2x﹣![]() ≤﹣3
≤﹣3![]() ,整数2x﹣
,整数2x﹣![]() 为﹣4,
为﹣4,
解得:x=﹣![]() ,
,
即原方程的解为:x=﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC和△CDE都是等腰直角三角形,∠C=90°,将△CDE绕点C逆时针旋转一个角度α(0°<α<90°),使点A,D,E在同一直线上,连接AD,BE.

(1)①依题意补全图2;
②求证:AD=BE,且AD⊥BE;
③作CM⊥DE,垂足为M,请用等式表示出线段CM,AE,BE之间的数量关系;
(2)如图3,正方形ABCD边长为 , 若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
, 若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B是直线m上两个定点,C是直线n上一个动点,且m∥n.以下说法:
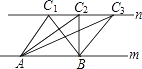
①△ABC的周长不变;
②△ABC的面积不变;
③△ABC中,AB边上的中线长不变.
④∠C的度数不变;
⑤点C到直线m的距离不变.
其中正确的有________(填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,⊙C的半径为r,点P是与圆心C不重合的点,给出如下定义:若点P′为射线CP上一点,满足CPCP′=r2 , 则称点P′为点P关于⊙C的反演点.右图为点P及其关于⊙C的反演点P′的示意图.

(1)如图1,当⊙O的半径为1时,分别求出点M(1,0),N(0,2),T( ,
,  )关于⊙O的反演点M′,N′,T′的坐标;
)关于⊙O的反演点M′,N′,T′的坐标;
(2)如图2,已知点A(1,4),B(3,0),以AB为直径的⊙G与y轴交于点C,D(点C位于点D下方),E为CD的中点.
①若点O,E关于⊙G的反演点分别为O′,E′,求∠E′O′G的大小;
②若点P在⊙G上,且∠BAP=∠OBC,设直线AP与x轴的交点为Q,点Q关于⊙G的反演点为Q′,请直接写出线段GQ′的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,O为坐标原点,点A的坐标为(1,a),点B的坐标为(b,1),点C的坐标为(c,0),其中a、b满足(a+b﹣8)2+|a﹣b+2|=0.
(1)求A、B两点的坐标;
(2)当△ABC的面积为6时,求点C的坐标;
(3)当4≤S△ABC≤10时,求点C的横坐标c的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴的单位长度为1,如果P,Q表示的数互为相反数,那么图中的4个点中,哪一个点表示的数的平方值最大( )

A. P B. R C. Q D. T
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)、菱形
 的边长1,面积为
的边长1,面积为 ,则
,则 的值为( )
的值为( )A、
 B、
B、 C、
C、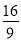 D、
D、
(2)、如图,ABCD是正方形,E是CF上一点,若DBEF是菱形,则∠EBC=

相关试题

