【题目】已知在平面直角坐标系中,O为坐标原点,点A的坐标为(1,a),点B的坐标为(b,1),点C的坐标为(c,0),其中a、b满足(a+b﹣8)2+|a﹣b+2|=0.
(1)求A、B两点的坐标;
(2)当△ABC的面积为6时,求点C的坐标;
(3)当4≤S△ABC≤10时,求点C的横坐标c的取值范围.
参考答案:
【答案】(1)A(1,3),B(5,1);(2)(1,0)或(13,0);(3)﹣3≤c≤3或11≤c≤17.
【解析】
(1)利用非负数的性质,把问题转化为方程组解决即可;
(2)分两种情形画出图形,分别构建方程即可解决问题;
(3)分两种情形分别构建不等式即可解决问题;
(1)∵(a+b﹣8)2+|a﹣b+2|=0.
∴![]() ,
,
解得![]() ,
,
∴A(1,3),B(5,1);
(2)①如图1中,当点C在直线AB的下方时,作AE⊥x轴于E,BF⊥x轴于F.设C(c,0).
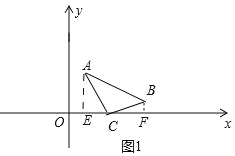
∵S△ABC=S四边形AEFB﹣S△AEC﹣S△BCF=![]() ×(1+3)×4﹣
×(1+3)×4﹣![]() ×3×(c﹣1)﹣
×3×(c﹣1)﹣![]() ×1×(5﹣c)=7﹣c,
×1×(5﹣c)=7﹣c,
∴7﹣c=6
解得c=1.
②如图2中,当点C在直线AB的上方时,作AE⊥x轴于E,BF⊥x轴于F.设C(c,0).
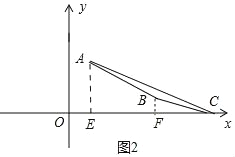
∵S△ABC=S△AEC﹣S四边形AEFB﹣S△BCF=![]() ×3×(c﹣1)﹣
×3×(c﹣1)﹣![]() ×(1+3)×4﹣
×(1+3)×4﹣![]() ×1×(c﹣5)=c﹣7,
×1×(c﹣5)=c﹣7,
∴c﹣7=6,
解得c=13,
∴满足条件的点C坐标为(1,0)或(13,0).
(3)由(2)可知,当点C在直线AB下方时,S△ABC=7﹣c,
∴4≤7﹣c≤10,
∴﹣3≤c≤3,
当点C在直线AB是上方时,S△ABC=c﹣7,
∴4≤c﹣7≤10,
∴11≤c≤17,
所以满足条件的c的取值范围为﹣3≤c≤3或11≤c≤17.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B是直线m上两个定点,C是直线n上一个动点,且m∥n.以下说法:
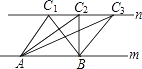
①△ABC的周长不变;
②△ABC的面积不变;
③△ABC中,AB边上的中线长不变.
④∠C的度数不变;
⑤点C到直线m的距离不变.
其中正确的有________(填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,⊙C的半径为r,点P是与圆心C不重合的点,给出如下定义:若点P′为射线CP上一点,满足CPCP′=r2 , 则称点P′为点P关于⊙C的反演点.右图为点P及其关于⊙C的反演点P′的示意图.

(1)如图1,当⊙O的半径为1时,分别求出点M(1,0),N(0,2),T( ,
,  )关于⊙O的反演点M′,N′,T′的坐标;
)关于⊙O的反演点M′,N′,T′的坐标;
(2)如图2,已知点A(1,4),B(3,0),以AB为直径的⊙G与y轴交于点C,D(点C位于点D下方),E为CD的中点.
①若点O,E关于⊙G的反演点分别为O′,E′,求∠E′O′G的大小;
②若点P在⊙G上,且∠BAP=∠OBC,设直线AP与x轴的交点为Q,点Q关于⊙G的反演点为Q′,请直接写出线段GQ′的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】设x是实数,现在我们用{x}表示不小于x的最小整数,如{3.2}=4,{﹣2.6}=﹣2,{4}=4,{﹣5}=5.在此规定下任一实数都能写出如下形式:x={x}﹣b,其中0≤b<1.
(1)直接写出{x}与x,x+1的大小关系是 (由小到大);
(2)根据(1)中的关系式解决下列问题:
①求满足{3x+11}=6的x的取值范围;
②解方程:{3.5x+2}=2x﹣
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴的单位长度为1,如果P,Q表示的数互为相反数,那么图中的4个点中,哪一个点表示的数的平方值最大( )

A. P B. R C. Q D. T
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)、菱形
 的边长1,面积为
的边长1,面积为 ,则
,则 的值为( )
的值为( )A、
 B、
B、 C、
C、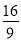 D、
D、
(2)、如图,ABCD是正方形,E是CF上一点,若DBEF是菱形,则∠EBC=

-
科目: 来源: 题型:
查看答案和解析>>【题目】程大位所著《算法统宗》是一部中国传统数学重要的著作.在《算法统宗》中记载:“平地秋千未起,踏板离地一尺.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”【注释】1步=5尺.
译文:“当秋千静止时,秋千上的踏板离地有1尺高,如将秋千的踏板往前推动两步(10尺)时,踏板就和人一样高,已知这个人身高是5尺.美丽的姑娘和才子们,每天都来争荡秋千,欢声笑语终日不断.好奇的能工巧匠,能算出这秋千的绳索长是多少吗?”
如图,假设秋千的绳索长始终保持直线状态,OA是秋千的静止状态,A是踏板,CD是地面,点B是推动两步后踏板的位置,弧AB是踏板移动的轨迹.已知AC=1尺,CD=EB=10尺,人的身高BD=5尺.设绳索长OA=OB=x尺,则可列方程为
相关试题

