搜索
【题目】如图，直线
、
相交于点
.
.
（1）求
的度数；
（2）以为端点引射线
、
，射线平分，且
，求
的度数.
参考答案：
【答案】（1）40°；（2）110°或70°.
【解析】
（1）由邻补角互补可得∠AOD+∠BOD=180°，已知
，由此可得2∠BOD+60°+∠BOD=180°，即可求得∠BOD=40°；（2）由角平分线的定义可得∠BOE=20°，再分两种情况求
的度数即可.
（1）由邻补角互补，可得∠AOD+∠BOD=180°，
∵
∴2∠BOD+60°+∠BOD=180°，
∴∠BOD=40°；
（2）如图：
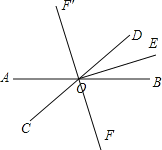
∵OE平分∠BOD，
∴∠BOE=
∠BOD=×40°=20°，
由角的和差得，∠BOF′=∠EOF′+∠BOE=90°+20°=110°，
∠BOF=∠EOF-∠BOE=90°-20°=70°．
∴的度数为110°或70°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形网格中，
、
、
均为格点(格点是指每个小正方形的顶点)，将
向下平移6个单位得到
.利用网格点和直尺画图：
（1）在网格中画出
；（2）画出
边上的中线
，
边上的高线
；（3）若
的边、分别与
的边
、
垂直，则的度数是 . -
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①a＜0；②
=1；③b2﹣4ac＜0；④当x＞1时，y随x的增大而减小；⑤当﹣1＜x＜3时，y＜0，其中正确的是_____．（只填序号）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，在Rt△ABC中，∠ACB＝90°，∠A＝30°，AB＝4，点D在直线BC上，E在AC上，且AC＝CD，DE＝AB．
（1）如图②，将△ECD沿CB方向平移，使点E落在AB上，得△E1C1D1，求平移的距离；
（2）如图③，将△ECD绕点C逆时针旋转，使点E落在AB上，得△E2CD2，求旋转角∠DCD2的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知
.
（1）如图1，
、
分别平分
、
.试说明:
；（2）如图2，若
，
，、分别平分
、
，那么
(只要直接填上正确结论即可). -
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两人分别骑自行车和摩托车，从同一地点沿相同的路线前往距离80km的某地，图中l1，l2分别表示甲、乙两人离开出发地的距离s（km）与行驶时间t（h）之间的函数关系．请根据图象解答下列问题：
（1）甲、乙两人谁到达目的地较早？早多长时间？
（2）分别求甲、乙两人行驶过程中s与t的函数关系式；
（3）试确定当两辆车都在行驶途中（不包括出发地和目的地）时，t的取值范围；并在这一时间段内，求t为何值时，摩托车行驶在自行车前面？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=﹣
﹣x+4，（1）用配方法确定它的顶点坐标、对称轴；
（2）x取何值时，y随x增大而减小？
（3）x取何值时，抛物线在x轴上方？
相关试题
