【题目】已知抛物线y=﹣![]() ﹣x+4,
﹣x+4,
(1)用配方法确定它的顶点坐标、对称轴;
(2)x取何值时,y随x增大而减小?
(3)x取何值时,抛物线在x轴上方?
参考答案:
【答案】(1)它的顶点坐标为(﹣1, ![]() ),对称轴为直线x=﹣1;(2)x>﹣1;(3)﹣4<x<2
),对称轴为直线x=﹣1;(2)x>﹣1;(3)﹣4<x<2
【解析】试题分析:(1)用配方法时,先提二次项系数,再配方,写成顶点式,根据顶点式的坐标特点求顶点坐标及对称轴;
(2)对称轴是x=-1,开口向下,根据对称轴及开口方向确定函数的增减性;
(3)令y=0,确定函数图象与x轴的交点,结合开口方向判断x的取值范围.
试题解析:(1)∵y=﹣![]() ﹣x+4=﹣
﹣x+4=﹣![]() (x2+2x﹣8)=﹣
(x2+2x﹣8)=﹣![]() [(x+1)2﹣9]=﹣
[(x+1)2﹣9]=﹣![]() +
+![]() ,
,
∴它的顶点坐标为(﹣1, ![]() ),对称轴为直线x=﹣1;
),对称轴为直线x=﹣1;
(2)∵抛物线对称轴是直线x=﹣1,开口向下,∴当x>﹣1时,y随x增大而减小;
(3)当y=0时,即﹣![]() +
+![]() =0解得x1=2,x2=﹣4,而抛物线开口向下,
=0解得x1=2,x2=﹣4,而抛物线开口向下,
∴当﹣4<x<2时,抛物线在x轴上方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A﹣C路径向终点C运动;点Q从B点出发沿B﹣C﹣A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.则点P运动时间为_________时,△PEC与△QFC全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题7分)如图,点B、F、C、E在一条直线上,FB=CE,AC=DF,请从下列三个条件:①AB=DE;②∠A=∠D;③∠ACB=∠DFE中选择一个合适的条件,使AB∥ED成立,并给出证明.

(1)选择的条件是 (填序号)
(2)证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.

(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)指出线段DC和线段BE的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠B=90°AB∥DF,AB=3cm,BD=8cm,点C是线段BD上一动点,点E是直线DF上一动点,且始终保持AC⊥CE。
(1)试说明:∠ACB =∠CED
(2)当C为BD的中点时,
 ABC与
ABC与 EDC全等吗?若全等,请说明理由;若不全等,请改变BD的长(直接写出答案),使它们全等。
EDC全等吗?若全等,请说明理由;若不全等,请改变BD的长(直接写出答案),使它们全等。(3)若AC=CE ,试求DE的长
(4)在线段BD的延长线上,是否存在点C,使得AC=CE,若存在,请求出DE的长及△AEC的面积;若不存在,请说明理由。





-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次函数y=kx+3中,y的值随着x值的增大而增大,请你写出符合条件的k的一个值: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程、计算
(1)
 (2)
(2)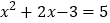 (限用配方法)
(限用配方法)(3) (x-2)
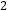 -5(x-2)-6=0 (4)计算、
-5(x-2)-6=0 (4)计算、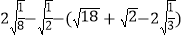
相关试题

