【题目】对平面直角坐标系中的点P(x,y),定义d=|x|+|y|,我们称d为P(x,y)的幸福指数.对于函数图象上任意一点P(x,y),若它的幸福指数d≥1恒成立,则称此函数为幸福函数,如二次函数y=x2+1就是一个幸福函数,理由如下:设P(x,y)为y=x2+1上任意一点,d=|x|+|y|=|x|+|x2+1|,∵|x|≥0,|x2+1|=x2+1≥1,∴d≥1.∴y=x2+1是一个幸福函数.
(1)若点P在反比例函数y=![]() 的图象上,且它的幸福指数d=2,请直接写出所有满足条件的P点坐标;
的图象上,且它的幸福指数d=2,请直接写出所有满足条件的P点坐标;
(2)一次函数y=﹣x+1是幸福函数吗?请判断并说明理由;
(3)若二次函数y=x2﹣(2m+1)x+m2+m(m>0)是幸福函数,试求出m的取值范围.
参考答案:
【答案】(1)满足条件的P点坐标为(﹣1,﹣1)或(1,1);
(2)一次函数y=﹣x+1是幸福函数,理由见解析;
(3)若二次函数y=x2﹣(2m+1)x+m2+m(m>0)是幸福函数,m的取值范围为m≥2.
【解析】试题分析:(1)设点P的坐标为(m, ![]() ),根据幸福指数的定义,即可得出关于m的分式方程,解之经检验即可得出结论;
),根据幸福指数的定义,即可得出关于m的分式方程,解之经检验即可得出结论;
(2)设P(x,y)为y=-x+1上的一点,分x<0、0≤x≤1和x>1三种情况找出d的取值范围,由此即可得出一次函数y=-x+1是幸福函数;
(3)设P(x,y)为y=x2-(2m+1)x+m2+m上的一点,由y=x2-(2m+1)x+m2+m=(x-m)(x-m-1)且m>0,可知分x≤0、0<x<m、m≤x≤m+1、x>m+1四段寻找m的取值范围,利用配方法以及二次函数的性质结合幸福函数的定义即可求出m的取值范围,综上即可得出结论.
试题解析:
解:(1)设点P的坐标为(m, ![]() ),
),
∴d=|m|+|![]() |=2,
|=2,
解得:m1=﹣1,m2=1,
经检验,m1=﹣1,m2=1是原分式方程的解,
∴满足条件的P点坐标为(﹣1,﹣1)或(1,1).
(2)一次函数y=﹣x+1是幸福函数,理由如下:
设P(x,y)为y=﹣x+1上的一点,d=|x|+|y|=|x|+|﹣x+1|,
当x<0时,d=|x|+|﹣x+1|=﹣x﹣x+1=1﹣2x>1;
当0≤x≤1时,d=|x|+|﹣x+1|=x﹣x+1=1;
当x>1时,d=|x|+|﹣x+1|=x+x﹣1=2x﹣1>1.
∴对于y=﹣x+1上任意一点P(x,y),它的幸福指数d≥1恒成立,
∴一次函数y=﹣x+1是幸福函数.
(3)设P(x,y)为y=x2-(2m+1)x+m2+m上的一点,d=|x|+|y|=|x|+|x2﹣(2m+1)x+m2+m|,
∵y=x2-(2m+1)x+m2+m=(x-m)(x-m-1),m>0,
∴分x≤0、0<x<m、m≤x≤m+1、x>m+1考虑.
①当x≤0时,d=|x|+|x2﹣(2m+1)x+m2+m|=﹣x+x2﹣(2m+1)x+m2+m=(x﹣m﹣1)2﹣m﹣1,
当x=0时,d取最小值,最小值为m2+m,
∴m2+m≥1,
解得:m≥![]() ;
;
②0<x<m时,d=|x|+|x2﹣(2m+1)x+m2+m|=x+x2﹣(2m+1)x+m2+m =(x﹣m)2+m﹣1≥1,
∵(x﹣m)2≥0,
∴m﹣1≥1,
解得:m≥2;
③当m≤x≤m+1时,d=|x|+|x2﹣(2m+1)x+m2+m|=x-x2+(2m+1)x-m2-m =﹣(x﹣m﹣1)2+m+1,
当x=m时,d取最小值,最小值为m,
∴m≥1;
④当x>m+1时,d=|x|+|x2﹣(2m+1)x+m2+m|=x+x2﹣(2m+1)x+m2+m=(x﹣m)2+m﹣1>m≥1,
∴m≥1.
综上所述:若二次函数y=x2-(2m+1)x+m2+m(m>0)是幸福函数,m的取值范围为m≥2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的序号是___.①当x=3时,EC<EM;②当y=9时,EC>EM③当x增大时,ECCF的值增大;④当y增大时,BEDF的值不变。
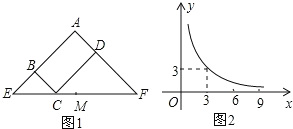
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错题进行整理、分析、改正”(选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)该调查的样本容量为________,
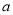 =________%,
=________%, 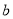 =________%,“常常”对应扇形的圆心角的度数为__________;
=________%,“常常”对应扇形的圆心角的度数为__________;(2)请你补全条形统计图;
(3)若该校有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的
学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让学生拓展视野、丰富知识,加深与自然和文化的亲近感,增加对集体生活方式和社会公共道德的体验,我区某中学决定组织部分师生去随州炎帝故里开展研学旅行活动.在参加此次活动的师生中,若每位老师带
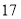 个学生,还剩
个学生,还剩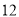 个学生没人带;若每位老师带
个学生没人带;若每位老师带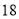 个学生,就有一位老师少带
个学生,就有一位老师少带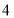 个学生.为了安全,既要保证所有师生都有车坐,又要保证每辆客车上至少要有
个学生.为了安全,既要保证所有师生都有车坐,又要保证每辆客车上至少要有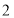 名老师.现有甲、乙两种大客车,它们的载客量和租金如表所示.
名老师.现有甲、乙两种大客车,它们的载客量和租金如表所示.
(1)参加此次研学旅行活动的老师有 人;学生有 人;租用客车总数为 辆;
(2)设租用
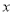 辆乙种客车,租车费用为
辆乙种客车,租车费用为 元,请写出
元,请写出 与
与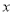 之间的函数关系式;
之间的函数关系式;(3)在(2)的条件下,学校计划此次研学旅行活动的租车总费用不超过
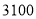 元,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
元,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2(m﹣1)x+m2﹣4=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为正整数,且该方程的两个根都是整数,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,直线y=
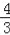 x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
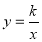 的图像与一次函数
的图像与一次函数 的图像的一个交点的横坐标是-3.
的图像的一个交点的横坐标是-3.(1)求
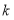 的值,并在指定坐标系中画出这两个函数的图像;
的值,并在指定坐标系中画出这两个函数的图像;(2)根据图像,直接写出使一次函数值大于反比例函数值时x的取值范围 .
相关试题

