搜索
【题目】学校计划选购甲、乙两种图书作为“校园读书节”的奖品．已知甲图书的单价是乙图书单价的
倍；用
元单独购买甲种图书比单独购买乙种图书要少
本．
（1）甲、乙两种图书的单价分别为多少元？
（2）若学校计划购买这两种图书共
本，且投入的经费不超过
元，要使购买的甲种图书数量不少于乙种图书的数量，则共有几种购买方案？
参考答案：
【答案】（1）、甲种图书的单价为30元，乙种图书的单价为20元；（2）、6种方案.
【解析】
试题分析：（1）、首先设乙种图书的单价为x元，则甲种图书的单价为1.5x元，然后根据数量关系列出分式方程，从而求出x的值，最后需要将x进行验根，得出答案；（2）、设购进甲种图书a本，则购进乙种图书（40﹣a）本，根据总费用和图书数量之间的关系列出不等式组，从而得出答案.
试题解析：（1）、设乙种图书的单价为x元，则甲种图书的单价为1.5x元，
由题意得：
﹣
=10
解得：x=20 经检验 ：x=20是原方程的解 则1.5x=30，
答：甲种图书的单价为30元，乙种图书的单价为20元；
、设购进甲种图书a本，则购进乙种图书（40﹣a）本，
根据题意得
解得：20≤a≤25， 所以共6种方案．
甲种图书 | 20 | 21 | 22 | 23 | 24 | 25 |
乙种图书 | 20 | 19 | 18 | 17 | 16 | 15 |
-
科目： 来源： 题型：
查看答案和解析>>【题目】己知反比例函数
（
常数，
）.（1）若点
在这个函数的图象上，求
的值;（2）若在这个函数图象的每一个分支上，
随
的增大而增大，求
的取值范围;（3）若
，试判断点
是否在这个函数的图象上，并说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点A（3，0），以A为圆心作⊙A与Y轴切于原点，与x轴的另一个交点为B，过B作⊙A的切线l．
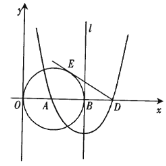
（1）以直线l为对称轴的抛物线过点A及点C（0，9），求此抛物线的解析式；
（2）抛物线与x轴的另一个交点为D，过D作⊙A的切线DE，E为切点，求DE的长；
（3）点F是切线DE上的一个动点，当△BFD与△EAD相似时，求出BF的长 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x，y的方程组
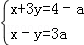，其中﹣3≤a≤1，给出下列命题：①
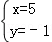是方程组的解；②当a=﹣2时，x，y的值互为相反数；
③当a=1时，方程组的解也是方程x+y=4﹣a的解；
④若x≤1，则1≤y≤4．
其中正确命题的序号是 ．（把所有正确命题的序号都填上）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角坐标系xOy中，A（﹣1，0），B（3，0），将A，B同时分别向上平移2个单位，再向右平移1个单位，得到的对应点分别为D，C，连接AD，BC．
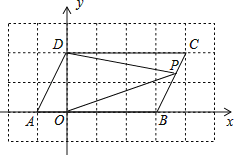
（1）直接写出点C，D的坐标：C ，D ；
（2）四边形ABCD的面积为 ；
（3）点P为线段BC上一动点（不含端点），连接PD，PO．求证：∠CDP+∠BOP=∠OPD．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在我市开展的“阳光体育”跳绳活动中，为了了解中学生跳绳活动的开展情况，随机抽查了全市七年级部分同学1分钟跳绳的次数，将抽查结果进行统计，并绘制两个不完整的统计图．请根据图中提供的信息，解答下列问题：
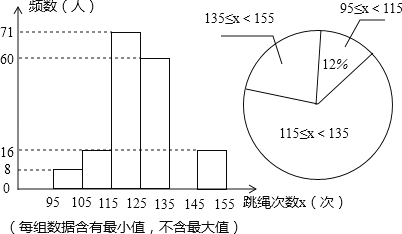
（1）本次共抽查了多少名学生？
（2）请补全频数分布直方图空缺部分，其中扇形统计图中表示跳绳次数范围135≤x＜155的扇形的圆心角度数为 度．
（3）若本次抽查中，跳绳次数在125次以上（含125次）为优秀，请你估计全市28000名七年级学生中有多少名学生的成绩为优秀？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，
的三个顶点坐标分别为A（2，-4），B（3，-2）， C（6，-3）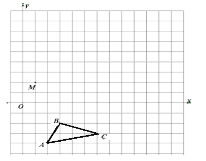
（1）画出△ABC关于
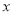轴对称的△A1B1C1；（2）以M点为位似中心，在网格中画出△A1B1C1的位似图形△A2B2C2 ，使△A2B2C2与△A1B1C1的相似比为2：1．
相关试题
