【题目】如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
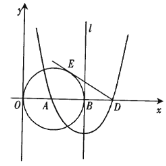
(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求DE的长;
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长 .
参考答案:
【答案】(1)y=![]() (x-6)2-3;(2)DE=3
(x-6)2-3;(2)DE=3![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
试题分析:(1)由题意可知,抛物线的对称轴为直线x=6,可设抛物线的解析式为y=a (x-6)2+k,将A,C两点坐标代入求a,k,即可确定该抛物线的解析式;(2)连接AE,可知∠AED=90°,AE=3 ,因为直线l是抛物线的对称轴,点A,D是抛物线与x轴的交点,所以AB=BD=3, AD=6 ,于是利用勾股定理可求出DE的长;(3)由题意可知,利用有两个角对应相等的两个三角形相似,切线DE上符合条件的F点有两个,即当BF⊥ED时和FB⊥AD时,利用相似三角形性质即可求出BF的长.
试题解析:(1)由题意可知,抛物线的对称轴为直线x=6,∴设抛物线的解析式为y=a (x-6)2+k,∵抛物线经过点A(3,0)和C(0,9),∴将A,C两点坐标代入得:![]() ,解得:a=
,解得:a=![]() ,k=-3.∴抛物线的解析式为y=
,k=-3.∴抛物线的解析式为y=![]() (x-6)2-3;(2)连接AE,∵DE是⊙A的切线,∴∠AED=90°,AE=3 ,∵直线l是抛物线的对称轴,点A,D是抛物线与x轴的交点,∴AB=BD=3,∴AD=6 , 在Rt△ADE中,DE2=AD2-AE2=62-32=27,∴DE=3
(x-6)2-3;(2)连接AE,∵DE是⊙A的切线,∴∠AED=90°,AE=3 ,∵直线l是抛物线的对称轴,点A,D是抛物线与x轴的交点,∴AB=BD=3,∴AD=6 , 在Rt△ADE中,DE2=AD2-AE2=62-32=27,∴DE=3![]() ;
;
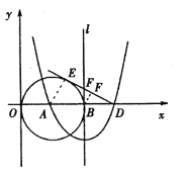
(3)利用有两个角对应相等的两个三角形相似,当BF⊥ED时,∵∠AED=∠BFD=90°,∠ADE=∠BDF,∴△AED∽△BFD,∴![]() ,即
,即![]() ,∴BF=
,∴BF=![]() .当FB⊥AD时,∵∠AED=∠FBD=90°,∠ADE=∠FDB,∴△AED∽△FBD , ∴
.当FB⊥AD时,∵∠AED=∠FBD=90°,∠ADE=∠FDB,∴△AED∽△FBD , ∴![]() 即BF=
即BF=![]()
![]() ,∴当△BFD与△EAD相似时,BF的长为
,∴当△BFD与△EAD相似时,BF的长为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1、l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是( )
A.2 B.3 C.4 D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽妈妈在网上做淘宝生意,专门销售女式鞋子,一次,小丽发现一个进货单上的一个信息是:A款鞋的进价比B款鞋进价多20元,花500元进A款鞋的数量和花400元进B款鞋的数量相同.
(1)问A、B款鞋的进价分别是多少元?
(2)小丽在销售单上记录了两天的数据如表:
日期
A款女鞋销量
B款女鞋销量
销售总额
6月1日
12双
8双
2240元
6月2日
8双
10双
1960元
请问两种鞋的销售价分别是多少?
(3)小丽妈妈说:“两款鞋的利润率相同”,请通过计算,结合(1)(2)所给信息,判断小丽妈妈的说法是否正确,如果正确,请说明理由;如果错误,能否只调整其中一款的售价,使得两款鞋的利润率相同?能否同时调整两款的售价,使得两款鞋的利润率相同?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知反比例函数
 (
( 常数,
常数, ).
).(1)若点

 在这个函数的图象上,求
在这个函数的图象上,求 的值;
的值;(2)若在这个函数图象的每一个分支上,
 随
随 的增大而增大,求
的增大而增大,求 的取值范围;
的取值范围;(3)若
 ,试判断点
,试判断点
 是否在这个函数的图象上,并说明理由.
是否在这个函数的图象上,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x,y的方程组
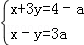 ,其中﹣3≤a≤1,给出下列命题:
,其中﹣3≤a≤1,给出下列命题:①
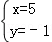 是方程组的解;
是方程组的解;②当a=﹣2时,x,y的值互为相反数;
③当a=1时,方程组的解也是方程x+y=4﹣a的解;
④若x≤1,则1≤y≤4.
其中正确命题的序号是 .(把所有正确命题的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划选购甲、乙两种图书作为“校园读书节”的奖品.已知甲图书的单价是乙图书单价的
 倍;用
倍;用 元单独购买甲种图书比单独购买乙种图书要少
元单独购买甲种图书比单独购买乙种图书要少 本.
本.(1)甲、乙两种图书的单价分别为多少元?
(2)若学校计划购买这两种图书共
 本,且投入的经费不超过
本,且投入的经费不超过 元,要使购买的甲种图书数量不少于乙种图书的数量,则共有几种购买方案?
元,要使购买的甲种图书数量不少于乙种图书的数量,则共有几种购买方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.
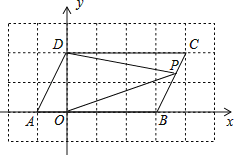
(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
相关试题

