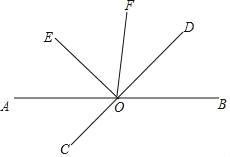
【题目】如图,直线AB、CD相交于点O,OE⊥OD,OE平分∠AOF.
(1)∠BOD与∠DOF相等吗?请说明理由.
(2)若∠DOF=![]() ∠BOE,求∠AOD的度数.
∠BOE,求∠AOD的度数.
参考答案:
【答案】(1)∠BOD=∠DOF,理由详见解析;(2)∠AOD=150°.
【解析】
(1)由OE⊥OD知∠EOF+∠DOF=90°,∠AOE+∠BOD=90°,根据∠AOE=∠EOF即可得∠BOD=∠DOF;
(2)由∠DOF=![]() ∠BOE可∠DOF=x°,则∠BOE=4x°,∠BOD=x°,从而得∠DOE=∠BOE﹣∠BOD=3x°,根据∠DOE=90°可得x的值,继而根据∠AOD=180°﹣∠BOD即可得出答案.
∠BOE可∠DOF=x°,则∠BOE=4x°,∠BOD=x°,从而得∠DOE=∠BOE﹣∠BOD=3x°,根据∠DOE=90°可得x的值,继而根据∠AOD=180°﹣∠BOD即可得出答案.
解:(1)∠BOD=∠DOF,
∵OE⊥OD,
∴∠DOE=90°,
∴∠EOF+∠DOF=90°,∠AOE+∠BOD=90°,
∵OE平分∠AOF,
∴∠AOE=∠EOF,
∴∠BOD=∠DOF;
(2)∵∠DOF=![]() ∠BOE,
∠BOE,
∴设∠DOF=x°,则∠BOE=4x°,∠BOD=x°,
∴∠DOE=∠BOE﹣∠BOD=3x°,
∵∠DOE=90°,
∴3x=90,即x=30,
∴∠BOD=30°,
∴∠AOD=180°﹣∠BOD=150°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣
 x2+bx+c交x轴于点A(2,0)、B(一8,0),交y轴于点C,过点A、B、C三点的⊙M与y轴的另一个交点为D.
x2+bx+c交x轴于点A(2,0)、B(一8,0),交y轴于点C,过点A、B、C三点的⊙M与y轴的另一个交点为D.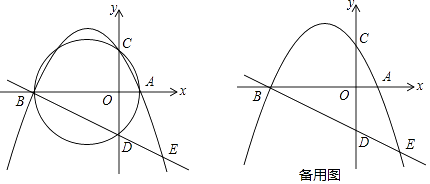
(1)求此抛物线的表达式及圆心M的坐标;
(2)设P为弧BC上任意一点(不与点B,C重合),连接AP交y轴于点N,请问:APAN是否为定值,若是,请求出这个值;若不是,请说明理由;
(3)延长线段BD交抛物线于点E,设点F是线段BE上的任意一点(不含端点),连接AF.动点Q从点A出发,沿线段AF以每秒1个单位的速度运动到点F,再沿线段FB以每秒 个单位的速度运动到点B后停止,问当点F的坐标是多少时,点Q在整个运动过裎中所用时间最少?
个单位的速度运动到点B后停止,问当点F的坐标是多少时,点Q在整个运动过裎中所用时间最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算:(a﹣b)2﹣a(a﹣2b);
(2)解方程: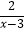 =
= 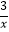 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某教育网站对下载资源规定如下:若注册VIP用户,则下载每份资源收
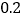 元,另外每年收500元的VIP会员费,若注册普通用户,则下载每份资源收
元,另外每年收500元的VIP会员费,若注册普通用户,则下载每份资源收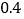 元,不收其它费用
元,不收其它费用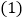 分别写出注册VIP用户的收费
分别写出注册VIP用户的收费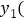 元
元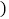 和注册普通用户
和注册普通用户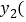 元
元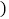 与下载数量
与下载数量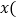 份
份 之间的函数关系式
之间的函数关系式 某学校每年要下载1500份资源,那么注册哪种用户比较合算?
某学校每年要下载1500份资源,那么注册哪种用户比较合算? 一年内下载多少份资源是两种用户收费一样?
一年内下载多少份资源是两种用户收费一样? -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:3+2=3×2-1,4+
 =4×
=4× -1,给出定义如下:
-1,给出定义如下:我们称使等式a+b=ab-1成立的一对有理数a,b为“椒江有理数对”,记为(a,b),如:数对(3,2),(4,
 )都是“椒江有理数对”.
)都是“椒江有理数对”.(1)数对(-2,1),(5,
 )中是“椒江有理数对”的是 ;
)中是“椒江有理数对”的是 ;(2)若(a,3)是“椒江有理数对”,求a的值;
(3)若(m,n)是“椒江有理数对”,则(-n,-m) “椒江有理数对”(填“是”、“不是”或“不确定”).
(4)请再写出一对符合条件的“椒江有理数对” (注意:不能与题目中已有的“椒江有理数对”重复)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段 AB=10cm,直线 AB 上有一点 C,且 BC=4cm,M 是线段 AC 的中点,则 AM 的长( )
A. 7cm B. 3cm C. 3cm 或 7cm D. 7cm 或 9cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)如图1,AD、BC相交于点O,OA=OC,∠OBD=∠ODB.求证:AB=CD.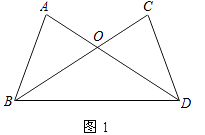
(2)如图2,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若OD=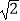 ,求∠BAC的度数.
,求∠BAC的度数. 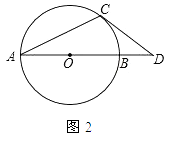
相关试题

