【题目】已知,如图,AB⊥OD,BD∥AC,AE,DE分别平分∠CAB,∠ODB,则∠AED=_________度

参考答案:
【答案】45.
【解析】
如图,由AC∥BD,得∠CAB=∠ABD,由AB⊥OD,得∠ABD+∠BDO=90°,即∠CAB+∠BDO=90°,即∠3+∠4+∠5+∠6=90°,过E作EF∥AC,可知BD∥AC∥EF,于是∠3=∠1,∠6=∠2,再由AE,DE分别平分∠CAB,∠ODB,得∠3=∠4=∠1,∠5=∠6=∠2,于是∠AED即可求得结果.
解:∵AC∥BD,∴∠CAB=∠ABD,
∵AB⊥OD,∴∠ABD+∠BDO=90°,
∴∠CAB+∠BDO=90°,
即∠3+∠4+∠5+∠6=90°,
过E作EF∥AC,

∵BD∥AC,
∴BD∥AC∥EF,
∴∠3=∠1,∠6=∠2,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠3=∠4=∠1,∠5=∠6=∠2,
∴∠AED=∠1+∠2=∠3+∠6=![]() ×90°=45°.
×90°=45°.
故答案为45.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解九年级学生的身体素质情况,随机抽查了九年级部分学生一分钟跳绳次数,绘制成如下统计图表(图1,图2,表).
等级
一分钟跳绳次数x
人数
A
x>180
12
B
150<x≤180
14
C
120<x≤150
a
D
x≤120
b

请结合图表完成下列问题:
(1)表1中a= ,b= ;
(2)请把图1和图2补充完整;
(3)已知该校有1000名九年级学生,若在一分钟内跳绳次数不大于120次的为不合格,则该校九年级学生一分钟跳绳不合格的学生估计为 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,CE平分∠BCD与AB交于点E,BF平分∠ABC与AD交于点F,若
 ,EF=4,则CD长为________.
,EF=4,则CD长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME = α,∠ABE = β,则 α 与 β 之间的数量关系为________.
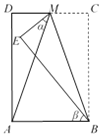
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的三个顶点的位置。如图所示,
现将△ABC平移后得△EDF,使点B的对应点为点D,点A对应点为点E.
(1)画出△EDF;
(2)线段BD与AE有何关系? ____________;
(3)连接CD、BD,则四边形ABDC的面积为_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80 m,DE=10 m,求障碍物B,C两点间的距离.(结果精确到0.1 m)(参考数据:
 ≈1.414,、
≈1.414,、 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=8,E为AB上一点,且AE=2,M为AD上一动点(不与A、D重合),AM=x,连结EM并延长交CD的延长线于F,过M作MG⊥EF交直线BC于点G,连结EG、FG.

(1)如图1,若M是AD的中点,求证:①△AEM≌△DFM;②△EFG是等腰三角形;
(2)如图2,当x为何值时,点G与点C重合?
(3)当x=3时,求△EFG的面积.
相关试题

