搜索
【题目】如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=80 m，DE=10 m，求障碍物B，C两点间的距离．(结果精确到0.1 m)（参考数据： 
≈1.414，、
≈1.732）
参考答案：
【答案】障碍物B，C两点间的距离约为52.7m.
【解析】试题分析：如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．通过解直角△AFD得到DF的长度；通过解直角△DCE得到CE的长度，则BC=BE-CE．
试题解析：如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．
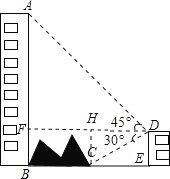
则DE=BF=CH=10m，
在直角△ADF中，∵AF=80m-10m=70m，∠ADF=45°，
∴DF=AF=70m．
在直角△CDE中，∵DE=10m，∠DCE=30°，
∴CE=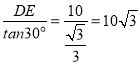
（m），
∴BC=BE-CE=70-10
≈70-17.32≈52.7（m）．
答：障碍物B，C两点间的距离约为52.7m．
-
科目： 来源： 题型：
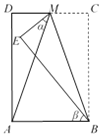
查看答案和解析>>【题目】如图，在长方形ABCD中，点M为CD中点，将△MBC沿BM翻折至△MBE，若∠AME ＝ α，∠ABE ＝ β，则 α 与 β 之间的数量关系为________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，AB⊥OD，BD∥AC，AE，DE分别平分∠CAB，∠ODB，则∠AED=_________度
-
科目： 来源： 题型：
查看答案和解析>>【题目】在正方形网格中，每个小正方形的边长都为1个单位长度，△ABC的三个顶点的位置。如图所示，
现将△ABC平移后得△EDF，使点B的对应点为点D，点A对应点为点E．
（1）画出△EDF；
（2）线段BD与AE有何关系？ ____________；
（3）连接CD、BD，则四边形ABDC的面积为_______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，AB=6，BC=8，E为AB上一点，且AE=2，M为AD上一动点（不与A、D重合），AM=x，连结EM并延长交CD的延长线于F，过M作MG⊥EF交直线BC于点G，连结EG、FG．
（1）如图1，若M是AD的中点，求证：①△AEM≌△DFM；②△EFG是等腰三角形；
（2）如图2，当x为何值时，点G与点C重合？
（3）当x=3时，求△EFG的面积．
-
科目： 来源： 题型：
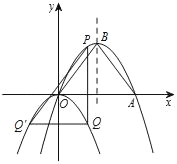
查看答案和解析>>【题目】如图，抛物线y=﹣
x2+bx+c经过原点和点A（6，0），与其对称轴交于点B，P是抛物线y=﹣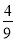
x2+bx+c上一动点，且在x轴上方．过点P作x轴的垂线交动抛物线y=﹣
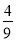（x﹣h）2（h为常数）于点Q，过点Q作PQ的垂线交动抛物线y=﹣
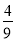（x﹣h）2于点Q′（不与点Q重合），连结PQ′，设点P的横坐标为m．（1）求抛物线y=﹣
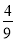x2+bx+c的函数关系式及点B的坐标；（2）当h=0时．
①求证：
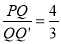；②设△PQQ′与△OAB重叠部分图形的周长为l，求l与m之间的函数关系式；
（3）当h≠0时，是否存在点P，使四边形OAQQ′为菱形？若存在，请直接写出h的值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线经过点A（﹣3，0）、B（0，3），C（1，0）．
（1）求抛物线及直线AB的函数关系式；
（2）有两动点D、E同时从O出发，以每秒1个单位长度的相同的速度分别沿线段OA、OB向A、B做匀速运动，过D作PD⊥OA分别交抛物线和直线AB于P、Q，设运动时间为t（0＜t＜3）．
①求线段PQ的长度的最大值；
②连接PE，当t为何值时，四边形DOEP是正方形；
③连接DE，在运动过程中，是否存在这样的t值，使PE=DE？若存在，请求出t的值；若不存在，请说明理由．
相关试题
