【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )
A.
B.
C.
D.
参考答案:
【答案】C
【解析】由翻折的性质得,∠CPD=∠C′PD,
∵PE平分∠BPC′,
∴∠BPE=∠C′PE,
∴∠BPE+∠CPD=90°,
∵∠C=90°,
∴∠CPD+∠PDC=90°,
∴∠BPE=∠PDC,
又∵∠B=∠C=90°,
∴△PCD∽△EBP,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴y= ![]() x(5﹣x)=﹣
x(5﹣x)=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴函数图象为C选项图象.
所以答案是:C.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
问题情境:如图1,在△ABC中,AB=AC,点D,E分别是边AB,AC上的点,且AD=AE,连接DE,易知BD=CE.将△ADE绕点A顺时针旋转角度α(0°<α<360°),连接BD,CE,得到图2.
(1)变式探究:如图2,若0°<α<90°,则BD=CE的结论还成立吗?若成立,请证明;若不成立,请说明理由;
(2)拓展延伸:若图1中的∠BAC=120°,其余条件不变,请解答下列问题:
从A,B两题中任选一题作答我选择 题
A.①在图1中,若AB=10,求BC的长;
②如图3,在△ADE绕点A顺时针旋转的过程中,当DE的延长线经过点C时,请直接写出线段AD,BD,CD之间的等量关系;
B.①在图1中,试探究BC与AB的数量关系,并说明理由;
②在△ADE绕点A顺时针旋转的过程中,当点D,E,C三点在同一条直线上时,请借助备用图探究线段AD,BD,CD之间的等量关系,并直接写出结果.

-
科目: 来源: 题型:
查看答案和解析>>【题目】新定义:若∠α的度数是∠β的度数的n倍,则∠α叫做∠β的n倍角.
(1)若∠M=10°21′,请直接写出∠M的3倍角的度数;
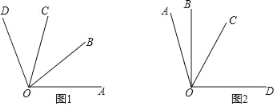
(2)如图1,若∠AOB=∠BOC=∠COD,请直接写出图中∠AOB的所有2倍角;
(3)如图2,若∠AOC是∠AOB的3倍角,∠COD是∠AOB的4倍角,且∠BOD=90°,求∠BOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种型号汽车油箱容量为40L,每行驶100km耗油10L.设一辆加满油的该型号汽车行驶路程为x(km),行驶过程中油箱内剩余油量为y(L)
(1)求y与x之间的函数表达式;
(2)为了有效延长汽车使用寿命,厂家建议每次加油时油箱内剩余油量不低于油箱容量的四分之一,按此建议,求该辆汽车最多行驶的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,E、F均为中点,则下列结论中:①AF⊥DE;②AD=BP;③PE+PF=
 PC;④PE+PF=PC.其中正确的是 .
PC;④PE+PF=PC.其中正确的是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC、直线l和格点O.
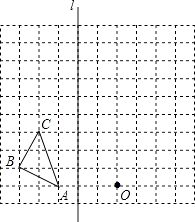
①画出△ABC关于直线l成轴对称的△A0B0C0;
②画出将△A0B0C0向上平移1个单位得到的△A1B1C1;
③以格点O为位似中心,将△A1B1C1作位似变换,将其放大到原来的两倍,得到△A2B2C2 . -
科目: 来源: 题型:
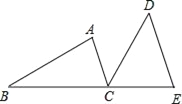
查看答案和解析>>【题目】如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
(1)求证:BC=DE
(2)若∠A=40°,求∠BCD的度数.
相关试题

