【题目】如图,正方形ABCD中,E、F均为中点,则下列结论中:①AF⊥DE;②AD=BP;③PE+PF= ![]() PC;④PE+PF=PC.其中正确的是 .
PC;④PE+PF=PC.其中正确的是 . 
参考答案:
【答案】①②③
【解析】解:如图1,
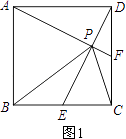
∵正方形ABCD,E,F均为中点,
∴AD=DC=BC,∠ADC=∠DCB,EC=DF= ![]() DC,
DC,
∵在△ADF和△DCE中, 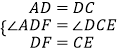 ,
,
∴△ADF≌△DCE(SAS),
∴∠AFD=∠DEC
∵∠DEC+∠CDE=90°
∴∠AFD+∠CDE=90°=∠DPF
∴AF⊥DE,∴①正确;
如图2,
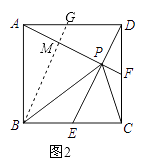
过B作BG∥DE交AD于G,交AP于M,
∵AF⊥DE,BG∥DE,E是BC中点,
∴BG⊥AP,G是AD的中点,
∴BG是AP的垂直平分线,
∴△ABP是等腰三角形
∴BP=AB=AD,∴②正确;
如图3,
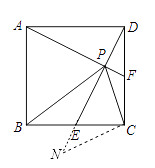
延长DE至N,使得EN=PF,连接CN,
∵∠AFD=∠DEC
∴∠CEN=∠CFP
又∵E,F分别是BC,DC的中点,
∴CE=CF,
∵在△CEN和△CFP中, 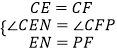 ,
,
∴△CEN≌△CFP(SAS),
∴CN=CP,∠ECN=∠PCF,
∵∠PCF+∠BCP=90°
∴∠ECN+∠BCP=∠NCP=90°
∴△NCP是等腰直角三角形
∴PN=PE+NE=PE+PF= ![]() PC,∴③正确,④错误;
PC,∴③正确,④错误;
∴①②③正确.
所以答案是:①②③.
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新定义:若∠α的度数是∠β的度数的n倍,则∠α叫做∠β的n倍角.
(1)若∠M=10°21′,请直接写出∠M的3倍角的度数;
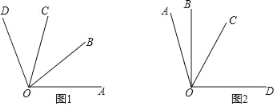
(2)如图1,若∠AOB=∠BOC=∠COD,请直接写出图中∠AOB的所有2倍角;
(3)如图2,若∠AOC是∠AOB的3倍角,∠COD是∠AOB的4倍角,且∠BOD=90°,求∠BOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种型号汽车油箱容量为40L,每行驶100km耗油10L.设一辆加满油的该型号汽车行驶路程为x(km),行驶过程中油箱内剩余油量为y(L)
(1)求y与x之间的函数表达式;
(2)为了有效延长汽车使用寿命,厂家建议每次加油时油箱内剩余油量不低于油箱容量的四分之一,按此建议,求该辆汽车最多行驶的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC、直线l和格点O.
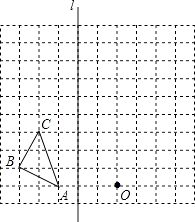
①画出△ABC关于直线l成轴对称的△A0B0C0;
②画出将△A0B0C0向上平移1个单位得到的△A1B1C1;
③以格点O为位似中心,将△A1B1C1作位似变换,将其放大到原来的两倍,得到△A2B2C2 . -
科目: 来源: 题型:
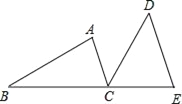
查看答案和解析>>【题目】如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
(1)求证:BC=DE
(2)若∠A=40°,求∠BCD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小亮分别从甲地和乙地同时出发,沿同一条路相向而行,小明开始跑步,中途改为步行,到达乙地恰好用
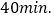 小亮骑自行车以
小亮骑自行车以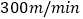 的速度直接到甲地,两人离甲地的路程
的速度直接到甲地,两人离甲地的路程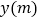 与各自离开出发地的时间
与各自离开出发地的时间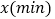 之间的函数图象如图所示,
之间的函数图象如图所示, 甲、乙两地之间的路程为______m,小明步行的速度为______
甲、乙两地之间的路程为______m,小明步行的速度为______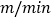 ;
; 求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围; 求两人相遇的时间.
求两人相遇的时间.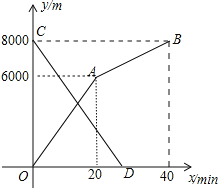
相关试题

