搜索
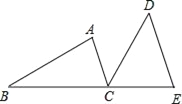
【题目】如图，B、C、E三点在同一条直线上，AC∥DE，AC=CE，∠ACD=∠B．
（1）求证：BC=DE
（2）若∠A=40°，求∠BCD的度数．
参考答案：
【答案】（1）证明见解析；（2）140°；
【解析】
（1）根据平行线的性质可得∠ACB=∠DEC，∠ACD=∠D，再由∠ACD=∠B可得∠D=∠B，然后可利用AAS证明△ABC≌△CDE，进而得到CB=DE；
（2）根据全等三角形的性质可得∠A=∠DCE=40°，然后根据邻补角的性质进行计算即可．
（1）∵AC∥DE，
∴∠ACB=∠DEC，∠ACD=∠D，
∵∠ACD=∠B．
∴∠D=∠B，
在△ABC和△DEC中，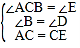
，
∴△ABC≌△CDE（AAS），
∴BC=DE；
（2）∵△ABC≌△CDE，
∴∠A=∠DCE=40°
∴∠BCD=180°–40°=140°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有一个直径为1m的圆形铁皮，要从中剪出一个最大的圆心角为90°的扇形ABC．
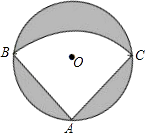
（1）求被剪掉阴影部分的面积；
（2）用所留的扇形铁皮围成一个圆锥，该圆锥的底面圆的半径是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】县内某小区正在紧张建设中，现有大量的沙石需要运输，“建安”车队有载重量为8吨、10吨的卡车共12辆，全部车辆运输一次能运输110吨沙石．
（1）求“建安”车队载重量为8吨、10吨的卡车各有多少辆？
（2）随着工程的进展，“建安”车队需要一次运输沙石165吨以上，为了完成任务，准备新增购这两种卡车共6辆，车队有多少种购买方案，请你一一写出． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，两直线AB，CD相交于点O，OE平分∠BOD，∠AOC∶∠AOD＝7∶11．
（1）求∠COE的度数；
（2）若OF⊥OE，求∠COF的度数．
-
科目： 来源： 题型：
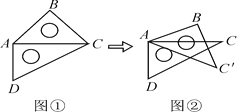
查看答案和解析>>【题目】取一副三角板按图①拼接，固定三角板ADC，将三角板ABC绕点A按顺时针方向旋转得到△ABC′，如图②所示．设∠CAC′＝α(0°＜α≤45°)．
（1）当α＝15°时，求证：AB∥CD；
（2）连接BD，当0°＜α≤45°时，∠DBC′＋∠CAC′＋∠BDC的度数是否变化，若变化 ，求出变化范围；若不变，求出其度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市某中学在创建“特色校园”的活动中，将本校的办学理念做成宣传牌（AB），放置在教学楼的顶部（如图所示）．小明在操场上的点D处，用1米高的测角仪CD，从点C测得宣传牌的底部B的仰角为37°，然后向教学楼正方向走了4米到达点F处，又从点E测得宣传牌的顶部A的仰角为45°．已知教学楼高BM=17米，且点A，B，M在同一直线上，求宣传牌AB的高度（结果精确到0.1米，参考数据：
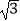≈1.73，sin37°≈0.60，cos37°≈0.81，tan37°≈0.75）．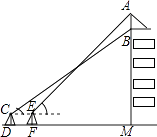
-
科目： 来源： 题型：
查看答案和解析>>【题目】探究题：
（1）三条直线相交，最少有__________个交点，最多有__________个交点，分别画出图形，并数出图形中的对顶角和邻补角的对数；
（2）四条直线相交，最少有__________个交点，最多有__________个交点，分别画出图形，并数出图形中的对顶角和邻补角的对数；
（3）依次类推，n条直线相交，最少有__________个交点，最多有__________个交点，对顶角有__________对，邻补角有__________对.
相关试题
