【题目】综合与探究
问题情境:如图1,在△ABC中,AB=AC,点D,E分别是边AB,AC上的点,且AD=AE,连接DE,易知BD=CE.将△ADE绕点A顺时针旋转角度α(0°<α<360°),连接BD,CE,得到图2.
(1)变式探究:如图2,若0°<α<90°,则BD=CE的结论还成立吗?若成立,请证明;若不成立,请说明理由;
(2)拓展延伸:若图1中的∠BAC=120°,其余条件不变,请解答下列问题:
从A,B两题中任选一题作答我选择 题
A.①在图1中,若AB=10,求BC的长;
②如图3,在△ADE绕点A顺时针旋转的过程中,当DE的延长线经过点C时,请直接写出线段AD,BD,CD之间的等量关系;
B.①在图1中,试探究BC与AB的数量关系,并说明理由;
②在△ADE绕点A顺时针旋转的过程中,当点D,E,C三点在同一条直线上时,请借助备用图探究线段AD,BD,CD之间的等量关系,并直接写出结果.

参考答案:
【答案】(1)结论:BD=CE.理由见解析;(2)A:①BC=10![]() .②结论:CD=
.②结论:CD=![]() AD+BD.理由见解析;B:①BC=
AD+BD.理由见解析;B:①BC=![]() AB.②结论:CD=
AB.②结论:CD=![]() AD+BD.理由见解析.
AD+BD.理由见解析.
【解析】
(1)结论:BD=CE.只要证明△DAB≌△EAC即可;
(2)A:①如图1中,作AH⊥BC于H.解直角三角形即可解决问题;
②结论:CD=![]() AD+BD.如图3中,作AH⊥CD于H.由△DAB≌△EAC,推出BD=CE,在Rt△ADH中,DH=ADcos30°=
AD+BD.如图3中,作AH⊥CD于H.由△DAB≌△EAC,推出BD=CE,在Rt△ADH中,DH=ADcos30°=![]() AD,由AD=AE,AH⊥DE,推出DH=HE,可得CD=DE+EC=2DH+BD=
AD,由AD=AE,AH⊥DE,推出DH=HE,可得CD=DE+EC=2DH+BD=![]() AD+BD;
AD+BD;
B:①如图1中,作AH⊥BC于H.解直角三角形可得:BC=2BH=![]() AB;
AB;
②类似A②;
(1)结论:BD=CE.
理由:如图2中,
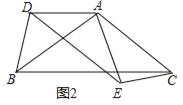
∵∠ABC=∠DAE,
∴∠DAB=∠EAC,
∵AD=AE,AB=AC,
∴△DAB≌△EAC,
∴BD=EC.
(2)A:①如图1中,作AH⊥BC于H.
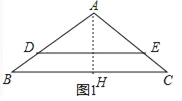
∵AB=AC,AH⊥BC,
∴BH=HC,
∵∠BAC=120°,
∴∠B=∠C=30°,
∴BH=ABcos30°=5![]() ,
,
∴BC=10![]() .
.
②结论:CD=![]() AD+BD.
AD+BD.
理由:如图3中,作AH⊥CD于H.
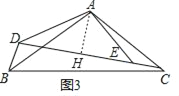
∵△DAB≌△EAC,
∴BD=CE,
在Rt△ADH中,DH=ADcos30°=AD,
∵AD=AE,AH⊥DE,
∴DH=HE,
∵CD=DE+EC=2DH+BD=![]() AD+BD.
AD+BD.
B:①如图1中,作AH⊥BC于H.
∵AB=AC,AH⊥BC,
∴BH=HC,
∵∠BAC=120°,
∴∠B=∠C=30°,
∴BH=ABcos30°=![]() AB,
AB,
∴BC=2BH=![]() AB.
AB.
②结论:CD=![]() AD+BD.
AD+BD.
证明方法同A②.
-
科目: 来源: 题型:
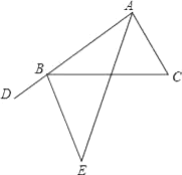
查看答案和解析>>【题目】完成下面证明:如图,B是射线AD上一点,∠DAE=∠CAE,∠DAC=∠C=∠CBE
(1)求证:∠DBE=∠CBE
证明:∵∠C=∠CBE(已知)
∴BE∥AC________
∴∠DBE=∠DAC________
∵∠DAC=∠C(已知)
∴∠DBE=∠CBE________
(2)请模仿(1)的证明过程,尝试说明∠E=∠BAE.
-
科目: 来源: 题型:
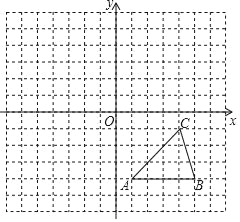
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为:A(1,﹣4),B(5,﹣4),C(4,﹣1).
(1)将△ABC经过平移得到△A1B1C1,若点C的应点C1的坐标为(2,5),写出点A,B的对应点A1,B1的坐标;
(2)在如图的坐标系中画出△A1B1C1,并画出与△A1B1C1关于原点O成中心对称的△A2B2C2.
-
科目: 来源: 题型:
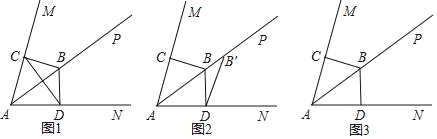
查看答案和解析>>【题目】如图1,已知射线AP是∠MAN的角平分线,点B为射线AP上的一点且AB=10,过点B分别作BC⊥AM于点C,作BD⊥AN于点D,BC=6.
(1)在图1中连接CD交AB于点O.求证:AB垂直平分CD;
(2)从A,B两题中任选一题作答,我选择 题
A.将图1中的△ABC沿射线AP的方向平移得到△ABC,点A、B、C的对应点分别为A′、B′、C′.若平移后点B的对应点B′的位置如图2,连接DB′.
①请在图2中画出此时的△A′B′C′,并在图中标注相应的字母;
②若图2中的DB′∥A′C′,写出平移的距离.
B.将图1中的△ABC沿射线AP的方向平移得到△A′B′C′,点A、B、C的对应点分别为A′、B′、C′.
①在△A′B′C′平移的过程中,若点C′与点D的连线恰好经过点B,请在图3中画出此时的△A′B′C′,并在图中标注相应的字母;
②如图3,点C′与点D的连线恰好经过点B,写出此时平移的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新定义:若∠α的度数是∠β的度数的n倍,则∠α叫做∠β的n倍角.
(1)若∠M=10°21′,请直接写出∠M的3倍角的度数;
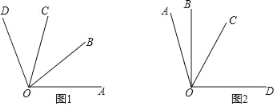
(2)如图1,若∠AOB=∠BOC=∠COD,请直接写出图中∠AOB的所有2倍角;
(3)如图2,若∠AOC是∠AOB的3倍角,∠COD是∠AOB的4倍角,且∠BOD=90°,求∠BOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种型号汽车油箱容量为40L,每行驶100km耗油10L.设一辆加满油的该型号汽车行驶路程为x(km),行驶过程中油箱内剩余油量为y(L)
(1)求y与x之间的函数表达式;
(2)为了有效延长汽车使用寿命,厂家建议每次加油时油箱内剩余油量不低于油箱容量的四分之一,按此建议,求该辆汽车最多行驶的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )

A.
B.
C.
D.
相关试题

